
Many times in our mathematical work we end up adding together a sequence of values such as
1 + 2 + 3 + 4 + ... + 30
20 + 21 + 22 + 23 + ... + 210
Notice that the values in the first sequence start at 1 and increase by 1 until we hit 30. The exponents in the second sequence start at 0 and increase by 1 until they hit 10. We have a special notation for indicating the sum of a sequence, if there is some part of that sequence which is increasing by 1 in each successive term. The notation is only useful in cases like the above where we have a starting value and an increment of 1. Here is another way of writing the sum 1 + 2 + 3 + ... + 30:

The Greek letter, sigma, stands for "sum". Below the sigma we put "i=1". This tells us that i is the name of the variable that is being incremented by 1 and that its starting value is 1. The number above the sigma is the final value of i. The i after the sigma is an expression that represents the form of each term in the sum. In this case, it is merely the values of i that are being added together. Here is another way of writing 20 + 21 + 22 + 23 + ... + 210:

In this case it is the exponent of the 2 that starts at 0 and goes up to 10.
There are some useful formulas for sums that you should add to your arsenal of mathematical weapons. For example, if you knew the formula

then you would know that the sum 1 + 2 + 3 + ... + 30 = (30 * 31)/2 = 930/2 = 465.
Here is a table of useful summation formulas:
 | 
|
 | 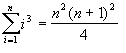
|
 | 
|
The idea of product notation is similar to that for sums. Whenever some part of a factor is increasing by 1, we can use product notation as a shorthand way of indicating a product. Consider the product
(1)(2)(3)...(7)
We can write this using product notation as follows:
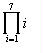
The only difference is that the symbol is a capital pi instead of a capital sigma. Product notation is used less often than summation notation, but you will occasionally see it in your work in computer science.