1. In Euclidean geometry (of the blackboard) from high school, named for Euclid of Alexandria (~325 BCE - 265 BCE), what is the sum of the angles in a triangle:
   (a) always 180 degrees
   (b) never 180 degrees
   (c) sometimes 180 degrees
   
   
   
   
2. In M.C. Escher's (1898-1972) hyperbolic space, the sum of the angles was
   (a) 180 degrees
   (b) 150 degrees
   (c) other
   
   
   
   Walking and folding an angle sum in Euclidean geometry
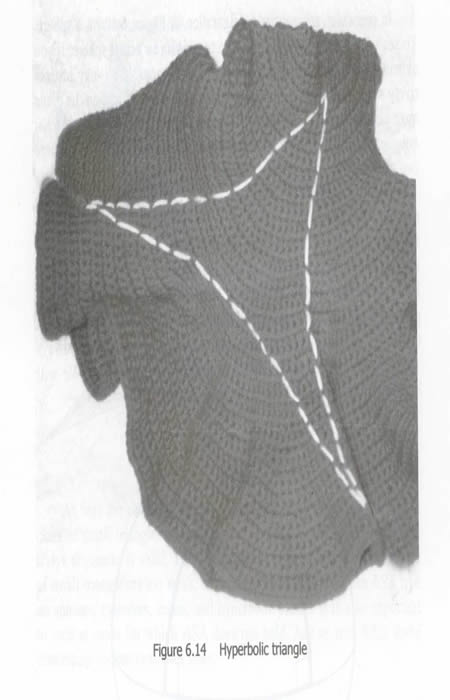
   Angle sum in the crochet model of hyperbolic geometry (Echer's space)
   
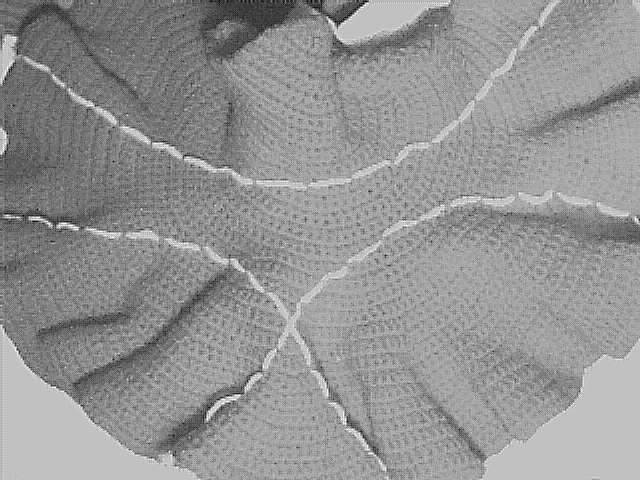
   Sketchpad Angle sum and Image of Angle sum
   discuss local (close to Euclidean geometry) to global (geometry is very different) perspectives
   
   
   
   
3. In perspective drawing and projective geometry, parallels from the real world
   (a) intersect in a vanishing point so there are zero parallels in this geometry
   (b) look parallel to the viewer
   (c) both answers are true
   
   
   
   
   
4. In Euclidean geometry John Playfair's (1748-1819) postulate that there is only one parallel to a line through a given point
   (a) always holds
   (b) never holds
   (c) sometimes holds
   
   
   
   
   
5. In Escher's hyperbolic space, John Playfair's (1748-1819) postulate that there is only one symmetric (symmetry!) path through a given point that never intersects a given symmetric path
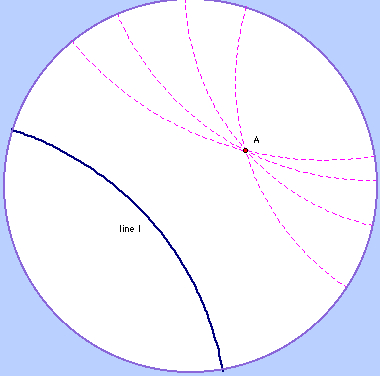
   (a) always holds
   (b) fails because there is more than one symmetric path that never intersects the original
   
   
   
   
   
6. In Euclidean geometry the Pythagorean theorem, named for Pythagoras of Samos (~569 BCE - 475 BCE)
   (a) holds because the sum of the squares of the bases surrounding a right angle equals the square of the hypotenuse of a right triangle
   (b) never holds
   (c) sometimes holds
   
   
   
   
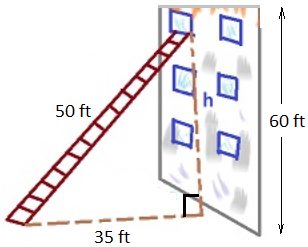
   Pythagorean theorem water demo