1. On Excel we see
    month   Payment   Interest   Principal   Loan Balance
    120 $58.18 $0.38 $57.80 ($0.63)
    What is the total amount paid on the loan? [NOT the total interest]
    1. $58.18
    2. $6981.60
    3. $6980.97
    4. other that can be derived from the given info
    5. no way to tell without more info




  2. In the derivation of the loan formula, we used:
    1. the bank earns interest on the lump sum amount while we pay it back via the periodic payment formula so that our payments plus resulting interest equals the lump sum amount plus interest.
    2. algebra of fractions, multiply, distibute, reciprocal and negative power
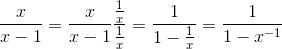      where x=(1+rate)n
    3. c) neither a) nor b)
    4. d) both a) and b)




  3. When the loan is set up so that there is a 0 balance in the Excel chart the last month, then we can calculate the total interest via two of the three methods:
    1. (monthly payment)(# payments) - (original loan)
    2. add the monthly interest for each and every month
    3. (original loan)(monthly rate)(#payments)

    Which is incorrect?
    1. method 1
    2. method 2
    3. method 3




  4. If we take out a $100 loan at 700% compounded monthly for 2 months, the monthly payment would be
    1. 100 (1 + 7/12)2
    2. 100((1 + 7/12)(2*12) - 1 ) / (7/12)
    3. 100 (7/12) / (1 - (1 + 7/12)(-2))
    4. other
    Answer the question and then write out a scenario for each of the other choices.



  5. If we pay an extra $20 each month on a loan then we will pay
    1. less total interest and I have a good reason why
    2. less total interest but I am unsure of why
    3. more total interest but I am unsure of why
    4. more total interest and I have a good reason why
    5. the same amount of interest