Some Partial Answers
Escher:
The sum of the angles in this work of art computes to 150 degrees so it is hyperbolic because it is less than 180 degrees.
Other works of Escher represent other geometries and the angle sum
computation distinguishes which geometry he represented.
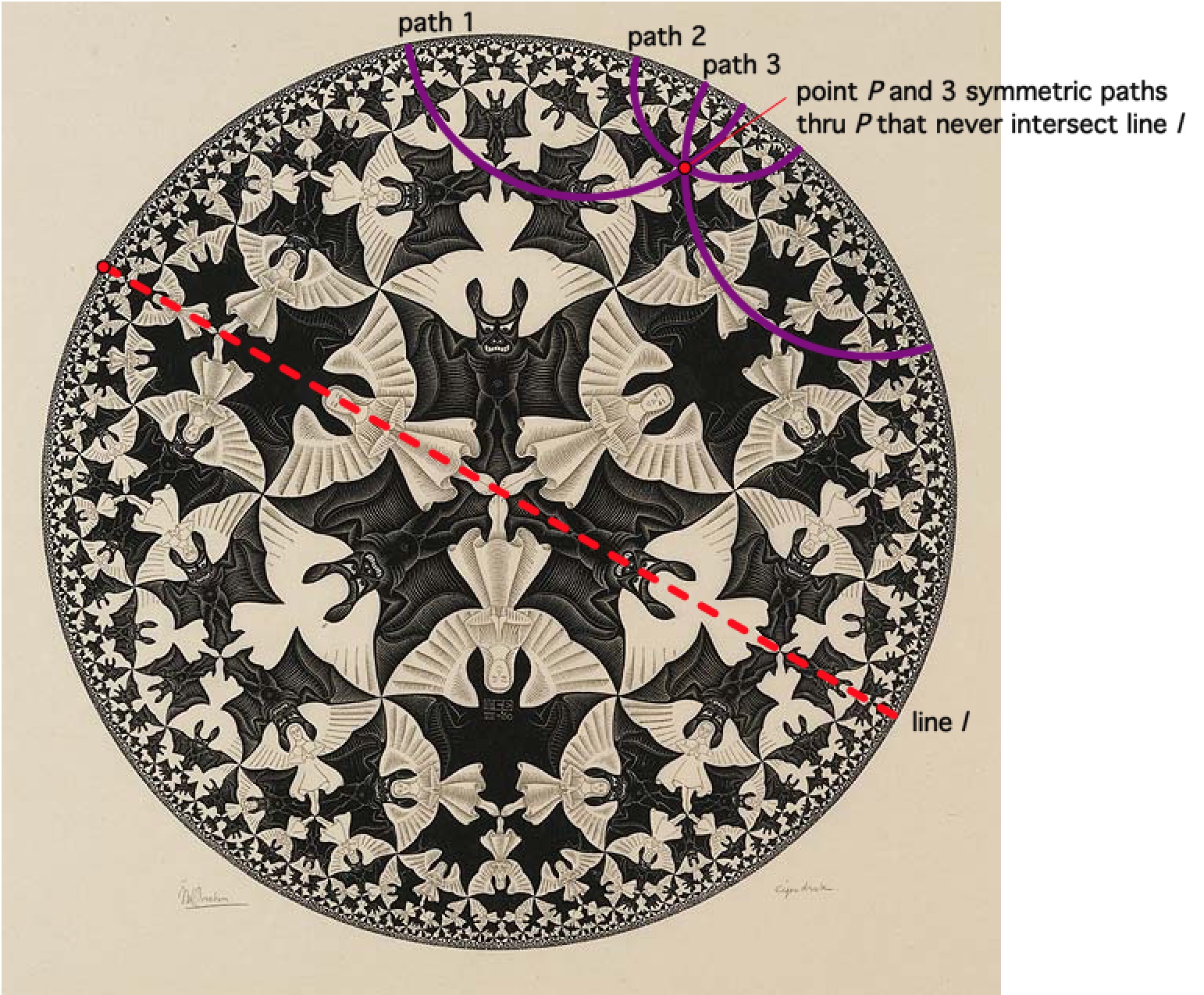
Paths cut creatures in half and we can draw more than one path in this work that goes through creatures and go through
a point off of such a symmetric path. In fact here is a sketch of 3 through point P that never intersect line l
Analyze the role of probability and chance in computing the density and geometry of the universe:
We can get such broad fluctuations in a Euclidean universe but only by chance 1 time in 3000, so from this perspective it is unlikely to be flat. Various margin of errors came up at the end of the Jeff Weeks video in terms of confidence intervals, the possibilities that the curvature and geometry of the universe was likely to range within, which included other geometries such as the spherical dodecahedron.
