 Image: Bryan Christie
|
Looking up at the sky on a clear night, we feel we can see forever. There seems to be no end to the stars and galaxies; even the darkness in between them is filled with light if only we stare through a sensitive enough telescope. In truth, of course, the volume of space we can observe is limited by the age of the universe and the speed of light. But given enough time, could we not peer ever farther, always encountering new galaxies and phenomena?
Maybe not. Like a hall of mirrors, the apparently endless universe might be deluding us. The cosmos could, in fact, be finite. The illusion of infinity would come about as light wrapped all the way around space, perhaps more than once--creating multiple images of each galaxy. Our own Milky Way galaxy would be no exception; bizarrely, the skies might even contain facsimiles of the earth at some earlier era. As time marched on, astronomers could watch the galaxies develop and look for new mirages. But eventually no new space would enter into their view. They would have seen it all.
The question of a finite or infinite universe is one of the oldest in philosophy. A common misconception is that it has already been settled in favor of the latter. The reasoning, often repeated in textbooks, draws an unwarranted conclusion from Einstein's general theory of relativity. According to relativity, space is a higher dimensional dynamic medium that can curve in one of three ways, depending on the distribution of matter and energy within it. Because we are embedded in space, we cannot see the flexure directly but rather perceive it as gravitational attraction and geometric distortion of images. To determine which of the three geometries our universe has, astronomers have been measuring the density of matter and energy in the cosmos. It now appears to be too low to force space to arch back on itself--a "spherical" geometry. Therefore, space must have either the familiar Euclidean geometry, like that of a plane, or a "hyperbolic" geometry, like that of Erdos' world. At first glance, such a universe stretches on forever.
One problem with this conclusion is that the universe could be a higher dimensional spherical shape, yet so large that the observable part seems Euclidean, just as a small patch of the earth's surface looks flat. A broader issue, however, is that relativity is a purely local theory. It predicts the curvature of each small volume of space--its geometry--based on the matter and energy it contains. Neither relativity nor standard cosmological observations say anything about how those volumes fit together to give the universe its overall shape--its topology. The three plausible cosmic geometries are consistent with many different topologies. For example, relativity would describe both a higher dimensional torus (a doughnutlike shape) and a Euclidean space with the same equations, even though the torus is finite and the plane is infinite. Determining the topology requires some physical understanding beyond relativity.
The usual assumption is that the universe is, like a plane, "simply connected," which means there is only one direct path for light to travel from a source to an observer. A simply connected Euclidean or hyperbolic universe would indeed be infinite. But the universe might instead be "multiply connected," like a torus, in which case there are many different such paths. An observer would see multiple images of each galaxy and could easily misinterpret them as distinct galaxies in an endless space, much as a visitor to a mirrored room has the illusion of seeing a huge crowd.
A multiply connected space is no mere mathematical whimsy; it is even preferred by some schemes for unifying the fundamental forces of nature, and it does not contradict any available evidence. Over the past few years, research into cosmic topology has blossomed. New observations may soon reach a definitive answer.
Many cosmologists expect the universe to be finite. Part of the reason may be simple comfort: the human mind encompasses the finite more readily than the infinite. But there are also two scientific lines of argument that favor finitude. The first involves a thought experiment devised by Isaac Newton and revisited by George Berkeley and Ernst Mach. Grappling with the causes of inertia, Newton imagined two buckets partially filled with water. The first bucket is left still, and the surface of the water is flat. The second bucket is spun rapidly, and the surface of the water is concave. Why?
The naive answer is centrifugal force. But how does the second bucket know it is spinning? In particular, what defines the inertial reference frame relative to which the second bucket spins and the first does not? Berkeley and Mach's answer was that all the matter in the universe collectively provides the reference frame. The first bucket is at rest relative to distant galaxies, so its surface remains flat. The second bucket spins relative to those galaxies, so its surface is concave. If there were no distant galaxies, there would be no reason to prefer one reference frame over the other. The surface in both buckets would have to remain flat, and therefore the water would require no centripetal force to keep it rotating. In short, it would have no inertia. Mach inferred that the amount of inertia a body experiences is proportional to the total amount of matter in the universe. An infinite universe would cause infinite inertia. Nothing could ever move.
In addition to Mach's argument, there is preliminary work in quantum cosmology, which attempts to describe how the universe emerged spontaneously from the void. Some such theories predict that a low-volume universe is more probable than a high-volume one. An infinite universe would have zero probability of coming into existence [see "Quantum Cosmology and the Creation of the Universe," by Jonathan J. Halliwell; Scientific American, December 1991]. Loosely speaking, its energy would be infinite, and no quantum fluctuation could muster such a sum.
Historically, the idea of a finite universe ran into its own obstacle: the apparent need for an edge. Aristotle argued that the universe is finite on the grounds that a boundary was necessary to fix an absolute reference frame, which was important to his worldview. But his critics wondered what happened at the edge. Every edge has another side. So why not redefine the "universe" to include that other side? German mathematician Georg F. B. Riemann solved the riddle in the mid-19th century. As a model for the cosmos, he proposed the hypersphere--the three-dimensional surface of a four-dimensional ball, just as an ordinary sphere is the two-dimensional surface of a three-dimensional ball. It was the first example of a space that is finite yet has no problematic boundary.
One might still ask what is outside the universe. But this question supposes that the ultimate physical reality must be a Euclidean space of some dimension. That is, it presumes that if space is a hypersphere, then that hypersphere must sit in a four-dimensional Euclidean space, allowing us to view it from the outside. Nature, however, need not cling to this notion. It would be perfectly acceptable for the universe to be a hypersphere and not be embedded in any higher-dimensional space. Such an object may be difficult to visualize, because we are used to viewing shapes from the outside. But there need not be an "outside."
By the end of the 19th century, mathematicians had discovered a variety of finite spaces without boundaries. German astronomer Karl Schwarzschild brought this work to the attention of his colleagues in 1900. In a postscript to an article in Vierteljahrschrift der Astronomischen Gesellschaft, he challenged his readers:
"Imagine that as a result of enormously extended astronomical experience, the entire universe consists of countless identical copies of our Milky Way, that the infinite space can be partitioned into cubes each containing an exactly identical copy of our Milky Way. Would we really cling on to the assumption of infinitely many identical repetitions of the same world?. . . We would be much happier with the view that these repetitions are illusory, that in reality space has peculiar connection properties so that if we leave any one cube through a side, then we immediately reenter it through the opposite side."
Schwarzschild's example illustrates how one can mentally construct a torus from Euclidean space. In two dimensions, begin with a square and identify opposite sides as the same--as is done in many video games, such as the venerable Asteroids, in which a spaceship going off the right side of the screen reappears on the left side. Apart from the interconnections between sides, the space is as it was before. Triangles span 180 degrees, parallel laser beams never meet and so on--all the familiar rules of Euclidean geometry hold. At first glance, the space looks infinite to those who live within it, because there is no limit to how far they can see. Without traveling around the universe and reencountering the same objects, the ship could not tell that it is in a torus. In three dimensions, one begins with a cubical block of space and glues together opposite faces to produce a 3-torus.
The Euclidean 2-torus, apart from some sugar glazing, is topologically equivalent to the surface of a doughnut. Unfortunately, the Euclidean torus is food only for the mind. It cannot sit in our three-dimensional Euclidean space. Doughnuts may do so because they have been bent into a spherical geometry around the outside and a hyperbolic geometry around the hole. Without this curvature, doughnuts could not be viewed from the outside.
When Albert Einstein published the first relativistic model of the universe in 1917, he chose Riemann's hypersphere as the overall shape. At that time, the topology of space was an active topic of discussion. Russian mathematician Aleksander Friedmann soon generalized Einstein's model to permit an expanding universe and a hyperbolic space. His equations are still routinely used by cosmologists. He emphasized that the equations of his hyperbolic model applied to finite universes as well as to the standard infinite one--an observation all the more remarkable because, at the time, no examples of finite hyperbolic spaces were known.
 Image: Bryan Christie
|
Of all the issues in cosmic topology, perhaps the most difficult to grasp is how a hyperbolic space can be finite. For simplicity, first consider a two-dimensional universe. Mimic the construction of a 2-torus but begin with a hyperbolic surface instead. Cut out a regular octagon and identify opposite pairs of edges, so that anything leaving the octagon across one edge returns at the opposite edge. Alternatively, one could devise an octagonal Asteroids screen. This is a multiply connected universe, topologically equivalent to a two-holed pretzel. An observer at the center of the octagon sees the nearest images of himself or herself in eight different directions. The illusion is that of an infinite hyperbolic space, even though this universe is really finite. Similar constructions are possible in three dimensions, although they are harder to visualize. One cuts a solid polyhedron out of a hyperbolic three-dimensional space and glues pairs of faces so that any object leaving from one face returns at the corresponding point on the matching face.
The angles of the octagon merit careful consideration. On a flat surface, a polygon's angles do not depend on its size. A large regular octagon and a small regular octagon both have inside angles of 135 degrees. On a curved surface, however, the angles do vary with size. On a sphere the angles increase as the polygon grows, whereas on a hyperbolic surface the angles decrease. The above construction requires an octagon that is just the right size to have 45-degree angles, so that when the opposite sides are identified, the eight corners will meet at a single point and the total angle will be 360 degrees. This subtlety explains why the construction would not work with a flat octagon; in Euclidean geometry, eight 135-degree corners cannot meet at a single point. The two-dimensional universe obtained by identifying opposite sides of an octagon must be hyperbolic. The topology dictates the geometry.
The size of the polygon or polyhedron is measured relative to the only geometrically meaningful length scale for a space: the radius of curvature. A sphere, for example, can have any physical size (in meters, say), but its surface area will always be exactly 4p times the square of its radius--that is, 4p square radians. The same principle applies to the size of a hyperbolic topology, for which a radius of curvature can also be defined. The most compact hyperbolic topology, discovered by one of us (Weeks) in 1985, may be constructed by identifying pairs of faces of an 18-sided polyhedron. It has a volume of approximately 0.94 cubic radian. Other topologies are built from larger polyhedra.
The universe, too, can be measured in units of radians. Diverse astronomical observations agree that the density of matter in the cosmos is only a third of that needed for space to be Euclidean. Either a cosmological constant makes up the difference [see "Cosmological Antigravity," by Lawrence M. Krauss; Scientific American, January], or the universe has a hyperbolic geometry with a radius of curvature of 18 billion light-years. In the latter case, the observable universe has a volume of 180 cubic radians--enough room for nearly 200 of the Weeks polyhedra. In other words, if the universe has the Weeks topology, its volume is only 0.5 percent of what it appears to be. As space expands uniformly, its proportions do not change, so the topology remains constant.
In fact, almost all topologies require hyperbolic geometries. In two dimensions, a finite Euclidean space must have the topology of either a 2-torus or a Klein bottle; in three dimensions, there are only 10 Euclidean possibilities--namely, the 3-torus and nine simple variations on it, such as gluing together opposite faces with a quarter turn or with a reflection, instead of straight across. By comparison, there are infinitely many possible topologies for a finite hyperbolic three-dimensional universe. Their rich structure is still the subject of intense research [see "The Mathematics of Three-Dimensional Manifolds," by William P. Thurston and Jeffrey R. Weeks; Scientific American, July 1984].
Despite the plethora of possibilities, the cosmologists of the 1920s had no way to measure the topology of the universe directly, and so they eventually lost interest in the issue. The decades from 1930 to 1990 were the dark ages of the subject. Most astronomy textbooks, quoting one another for support, stated that the universe must be either a hypersphere, an infinite Euclidean space or an infinite hyperbolic space. Other topologies were largely forgotten. But the 1990s have seen the rebirth of the subject. Roughly as many papers have been published on cosmic topology in the past three years as in the preceding 80. Most exciting of all, cosmologists are finally poised to determine the topology observationally.
The simplest test of topology is to look at the arrangement of galaxies. If they lie in a rectangular lattice, with images of the same galaxy repeating at equivalent lattice points, the universe is a 3-torus. Other patterns reveal more complicated topologies. Unfortunately, looking for such patterns is difficult, because the images of a galaxy would depict different points in its history. Astronomers would need to recognize the same galaxy despite changes in appearance or shifts in position relative to neighboring galaxies. Over the past 25 years researchers such as Dmitri Sokoloff of Moscow State University, Viktor Shvartsman of the Soviet Academy of Sciences, J. Richard Gott III of Princeton University and Helio V. Fagundes of the Institute for Theoretical Physics in São Paulo have looked for and found no repeating images among galaxies within one billion light-years of the earth.
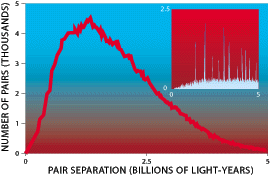 Image: Bryan Christie
|
Roland Lehoucq and Marc Lachièze-Rey of the Center for Astrophysical Studies in Saclay, France, together with one of us (Luminet), have tried to circumvent the problems of galaxy recognition in another way. We have developed the method of cosmic crystallography, which in a Euclidean universe can make out a pattern statistically without needing to recognize specific galaxies as images of one another. If galaxy images repeat periodically, a histogram of all galaxy-to-galaxy distances should show peaks at certain distances, which represent the true size of the universe. So far we have seen no patterns, but this may be because of the paucity of data on galaxies farther away than two billion light-years. The Sloan Digital Sky Survey--an ongoing American-Japanese collaboration to prepare a three-dimensional map of much of the universe--will produce a larger data set for these studies.
Finally, several other research groups plan to ascertain the topology of the universe using the cosmic microwave background, the faint glow remaining from the time when the primordial plasma of the big bang condensed to hydrogen and helium gas. The radiation is remarkably homogeneous: its temperature and intensity are the same in all parts of the sky to nearly one part in 100,000. But there are slight undulations discovered in 1991 by the Cosmic Background Explorer (COBE) satellite. Roughly speaking, the microwave background depicts density variations in the early universe, which ultimately seeded the growth of stars and galaxies [see "The Evolution of the Universe," by P. James E. Peebles, David N. Schramm, Edwin L. Turner and Richard G. Kron; Scientific American, October 1994].
These fluctuations are the key to resolving a variety of cosmological issues, and topology is one of them. Microwave photons arriving at any given moment began their journeys at approximately the same time and distance from the earth. So their starting points form a sphere, called the last scattering surface, with the earth at the center. Just as a sufficiently large paper disk overlaps itself when wrapped around a broom handle, the last scattering surface will intersect itself if it is big enough to wrap all the way around the universe. The intersection of a sphere with itself is simply a circle of points in space.
Looking at this circle from the earth, astronomers would see two circles in the sky that share the same pattern of temperature variations. Those two circles are really the same circle in space seen from two perspectives. They are analogous to the multiple images of a candle in a mirrored room, each of which shows the candle from a different angle.
Two of us (Starkman and Weeks), working with David N. Spergel and Neil J. Cornish of Princeton, hope to detect such circle pairs. The beauty of this method is that it is unaffected by the uncertainties of contemporary cosmology--it relies on the observation that space has constant curvature but makes no assumptions about the density of matter, the geometry of space or the presence of a cosmological constant. The main problem is to identify the circles despite the forces that tend to distort their images. For example, as galaxies coalesce, they exert a varying gravitational pull on the radiation as it travels toward the earth, shifting its energy.
Unfortunately, COBE was incapable of resolving structures on an angular scale of less than 10 degrees. Moreover, it did not identify individual hot or cold spots; all one could say for sure is that statistically some of the fluctuations were real features rather than instrumental artifacts. Higher-resolution and lower-noise instruments have since been developed. Some are already making observations from ground-based or balloon-borne observatories, but they do not cover the whole sky. The crucial observations will be made by the National Aeronautics and Space Administration's Microwave Anisotropy Probe (MAP), due for launch late next year, and the European Space Agency's Planck satellite, scheduled for 2007.
The relative positions of the matching circles, if any, will reveal the specific topology of the universe. If the last scattering surface is just barely big enough to wrap around the universe, it will intersect only its nearest ghost images. If it is larger, it will reach farther and intersect the next nearest images. If the last scattering surface is large enough, we expect hundreds or even thousands of circle pairs. The data will be highly redundant. The largest circles will completely determine the topology of space as well as the position and orientation of all smaller circle pairs. Thus, the internal consistency of the patterns will verify not only the correctness of the topological findings but also the correctness of the microwave background data.
Other teams have different plans for the data. John D. Barrow and Janna J. Levin of the University of Sussex, Emory F. Bunn of Bates College, and Evan Scannapieco and Joseph I. Silk of the University of California at Berkeley intend to examine the pattern of hot and cold spots directly. The group has already constructed sample maps simulating the microwave background for particular topologies. They have multiplied the temperature in each direction by the temperature in every other direction, generating a huge four-dimensional map of what is usually called the two-point correlation function. The maps provide a quantitative way of comparing topologies. J. Richard Bond, Dmitry Pogosyan and Tarun Souradeep of the Canadian Institute for Theoretical Astrophysics are applying related new techniques to the existing COBE data, which could prove sufficiently accurate to identify the smallest hyperbolic spaces.
Beyond the immediate intellectual satisfaction, discovering the topology of space would have profound implications for physics. Although relativity says nothing about the universe's topology, newer and more comprehensive theories that are under development should predict the topology or at least assign probabilities to the various possibilities. These theories are needed to explain gravity in the earliest moments of the big bang, when quantum-mechanical effects were important [see "Quantum Gravity," by Bryce S. DeWitt; Scientific American, December 1983]. The theories of everything, such as string theory, are in their infancy and do not yet have testable consequences. But eventually the candidate theories will make predictions about the topology of the universe on large scales.
The tentative steps toward the unification of physics have already spawned the subfield of quantum cosmology. There are three basic hypotheses for the birth of the universe, which are advocated, respectively, by Andrei Linde of Stanford University, Alexander Vilenkin of Tufts University and Stephen W. Hawking of the University of Cambridge. One salient point of difference is whether the expected volume of a newborn universe is very large (Linde's and Vilenkin's proposals) or very small (Hawking's). Topological data may be able to distinguish among these models.
If observations do find the universe to be finite, it might help to resolve a major puzzle in cosmology: the universe's large-scale homogeneity. The need to explain this uniformity led to the theory of inflation, but inflation has run into difficulty of late, because in its standard form it would have made the cosmic geometry Euclidean--in apparent contradiction with the observed matter density. This conundrum has driven theorists to postulate hidden forms of energy and modifications to inflation [see "Inflation in a Low-Density Universe," by Martin A. Bucher and David N. Spergel; Scientific American, January]. An alternative is that the universe is smaller than it looks. If so, inflation could have stopped prematurely--before imparting a Euclidean geometry--and still have made the universe homogeneous. Igor Y. Sokolov of the University of Toronto and others have used COBE data to rule out this explanation if space is a 3-torus. But it remains viable if space is hyperbolic.
Since ancient times, cultures around the world have asked how the universe began and whether it is finite or infinite. Through a combination of mathematical insight and careful observation, science in this century has partially answered the first question. It might begin the next century with an answer to the second as well.
JEAN-PIERRE LUMINET, GLENN D. STARKMAN and JEFFREY R. WEEKS say they relish participating in the boom years of cosmic topology, as researchers come together across disciplinary boundaries and no question is considered stupid. Luminet, who studies black holes at Paris Observatory, has written several books of science and of poetry and collaborated with composer Gérard Grisey on the musical performance Le Noir de l'Etoile. Starkman was institutionalized for six years--at the Institute for Advanced Study in Princeton, N.J., and then at the Canadian Institute for Theoretical Astrophysics in Toronto. He has been released into the custody of Case Western Reserve University in Cleveland. Weeks, the mathematician of the trio, resigned his position at Ithaca College to care for his newborn son and now receives funding from the National Science Foundation to develop research software.