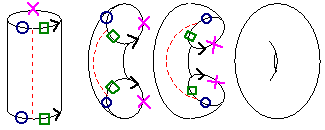


 Play Button to watch
Davide Cervone's
Folding Cube Movie and then re-read the explanation above.
Notice that you can use the other buttons to play it slide by slide
or to rewind or replay the movie.
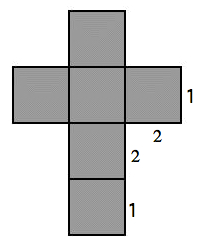
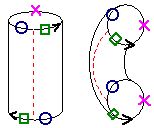
Label gluing instructions on the figure to show
which sides you would glue together in order to form a cube. (Hint: You will
need to glue 7 sets of edges together, so you may want to give the
instructions by labeling a set of 1s to be glued together, a set of 2s,
and so on...) We could give these gluing instructions to
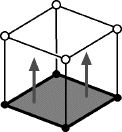
Marge and explain that
while the figure can't be glued in 2D,
there is
enough room to perform the gluing in 3D.
Play Button to watch
Davide Cervone's
Folding Cube Movie and then re-read the explanation above.
Notice that you can use the other buttons to play it slide by slide
or to rewind or replay the movie.
Label gluing instructions on the figure to show
which sides you would glue together in order to form a cube. (Hint: You will
need to glue 7 sets of edges together, so you may want to give the
instructions by labeling a set of 1s to be glued together, a set of 2s,
and so on...) We could give these gluing instructions to
Marge and explain that
while the figure can't be glued in 2D,
there is
enough room to perform the gluing in 3D.