2D Universes Lab

We began the semester by discussing how we represent our earth, and we are now exploring how we can represent other kinds of worlds and universes, like the world of perspective drawing, Escher's artistic works, and maps and Pac-Man's universe. We'll continue this exploration today by discussing how we can represent 2D universes.

As in the homework pre-readings experts think that the universe might have many more physical dimensions than we directly experience. In order to try and understand the idea of more physical dimensions, we will step back and try to address an easier, but related question: How could a 2D creature understand the 3rd dimension? In the process, we will see some ideas that at first appear counterintuitive. We will look at 3D objects in new ways in an attempt to develop visualization skills that we will need in order to understand the 4th physical dimension and the shape of the universe. We previously explored Homer's transition in Homer3. For now, assume that the Simpsons really were 2D creatures living in an x-y plane of some blackboard and that Homer had made the transformation to a 3D creature. While the 2D Simpsons folks can't really understand the 3rd dimension and would feel like there isn't any room for another dimension, they could see weird behavior occurring that suggests that the 3rd dimension exists (for example the "wall" that Homer disappeared into could not be explained using only 2 dimensions). Homer's wife, 2D Marge, wouldn't be able to comprehend the concept of depth or an entire 3D Homer, since only 2D pieces would make sense to her.
Read through the following text, take notes for yourself and answer the questions after discussing them with a neighbor
  1. How could 2D Marge and 2D Lisa "pass" each other? (Hint: Think of them moving around in their 2D plane of existence that has no depth - they can't pass by each other like we do since they would bump into each other.)


  2. In order to explain a cube to 2D folks and to Homer Simpson, who is trapped in the "third" dimension, a 2D Professor Frink says:
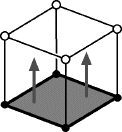
    Frink: -- but suppose we exte-end the square beyond the two dimensions of our universe (along the hypothetical z-axis, there).
    Everyone: [gasps]
    Frink: This forms a three-dimensional object known as a "cube", or a "Frinkahedron" in honor of its discoverer, n'hey, n'hey.
    (Taken from text transcript of 3D Homer segment and Did You Notice? by James A. Cherry)
    On the "Frinkahedron", label the z-axis

  3. There is an alternative way of forming a cube - by gluing edges together.
    Before we try to glue a cube, let's do an easier example together. We can form a cylinder by taking a piece of paper and gluing 2 opposite sides together (try this). We could explain this to 2D Marge by drawing a square and then telling her the left and right side are glued.
    While she wouldn't understand how there could be space to accomplish this feat, (since we need a 3rd dimension to actually glue the edges together to form the cylinder), nor could she see the square like we do (she could only see the outside edges of it as she climbed around it) she could still comprehend the gluing instructions of the edges.
    From Davide Cervone's Folding Cubes and Hypercubes:
    "The following movie shows an unfolded cube (red) in space, together with its shadow (pink) on the plane below. The white dot at the top of the image represents the light source. As the red cube folds up, we can follow the results in the shadow below. As the sides of the cube begin to fold up, the shadows of these squares become distorted (one edge is closer to the light than the opposite edge, so one edge has a larger shadow than the other).... We rotate the whole arrangement so that we see only the shadow of the cube and must imagine the three-dimensional cube unfolding that causes these shadows." After you click on the link on today's lab, use the Play Button to watch Davide Cervone's Folding Cube Movie.
  4. Sketch the figure and label gluing instructions to show which sides you would glue together in order to form a cube. I have started you off by labeling a set of 1s to be glued to each other, and a set of 2s. You will need to glue 5 more sets of edges together, so give the instructions by labeling two 3s that glue together, 4s, 5s, 6s, and 7s. We could give these gluing instructions to Marge or Arthur Square and explain that while the figure can't be glued in 2D, there is enough room to perform the gluing in 3D.


  5. The Shape of a 2D Universe A 2D creature could live on many differently shaped universes, such as the surface of a sphere (a spherical universe) or a blackboard (a Euclidean universe). Here are some additional possibilities:

    Torus - A Euclidean Universe A torus is a mathematician's name for a donut. The surface of a torus is the topological space found in old-style video games such as Pac Man, where a spaceship goes off the right-hand side of the screen only to reappear on the left, or off the top to reappear on the bottom.
    If you take a sheet and try to glue the left edge to the right edge (the single arrows tell you to do this) and the top edge to the bottom edge (the double arrows tell you to do this), the paper will crumple up and you'll get a big mess.
    But, we can do this identification of a square with a stretchy piece of rubber. First we identify the left and right hand side in order to form a cylinder. We use these arrows and the points that correspond to glue the top and the bottom together and this forms a donut or torus.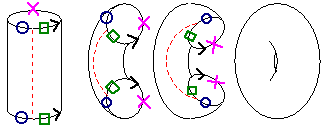
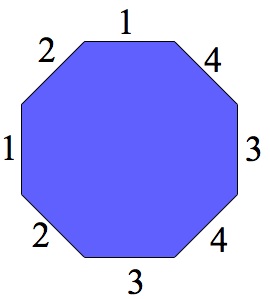
    2-Holed Donut - A Hyperbolic Universe
    Here we glue the side with a number on it with the side that has the same number on it. It is an exercise in visualization skills to see that the resulting figure is a 2-holed donut. Here are directions for sewing the 2-holed donut that may be helpful for visual purposes.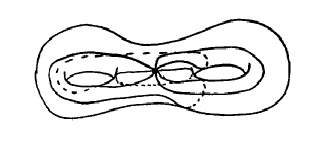
  6. Search the web to find the measure of one interior angle of a flat octagon ______________

    To understand why the laws of Euclidean geometry that you learned in high school do not apply to the 2-holed donut, we can look to see whether octagons will tile the plane in the same way that Escher created his works of art. So we would like to know whether we can take a certain number of octagons (instead of angles and devils like Escher used in the distorted hyperbolic     Heaven and Hell work...) and put them together around a vertex in order to form 360 degrees.
  7. How much of 360 degrees is left over at the red vertex when two octagons are placed side by side--the leftover angle is indicated by the green arc?
    ___________

  8. What happens if you try and place three octagons together at a vertex? Do they fit into 360 degrees? ______
    If so, we could create a flat tiling work of art (like Escher) without distorting them. If not, then we must distort them in order to create a flat work of art.

    We can create a 2-holed donut by using a distorted octagon with 45 degree interior angles. Eight of these glue together in a space that looks like Escher's work to form 360 degrees at a vertex and so they tile the space. Now we understand some of the issues that Escher faced and why his Heaven and Hell work looked like it did.


  9. Klein Bottle - A Euclidean Universe
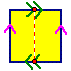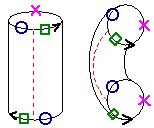
    Notice that this identification labeling of a square looks similar to the one that resulted in a torus (donut), but the top and bottom edges are glued with a twist - a reflection in the line between the midpoints of the sides. Just as a 2D Flatlander could not imagine how to construct a cylinder out of a piece of paper, we have problems figuring out how to put together this square, because when we label corresponding points (such as the green squares, which are the same in this space because they are identified via the reflection in the dotted line), there seems to be no way to glue them together. However, an inhabitant of 4-space would have no trouble because he would have enough space to glue the edges together.
    Forming the Klein bottle slinky. There is only one way to for us to put this space together in 3D- by having a slinky intersect itself by passing through itself. I have a glass Klein bottle in my office. I'll come around to show you this gluing.

  10. Did you understand how the gluing instructions formed the Klein bottle and why they don't result in a torus (donut)? If the answer is no, ask me as I make my way around. ___________


    11. Klein bottle
    The space that we have represented here has a nasty intersection when the slinky passes through itself. Our gluing instructions give no hint of this and in fact, the intersections only arose when we tried to glue the space in 3 dimensions. In order to properly see an actual model of the glued square, we would really need a 4th physical dimension. In the 4th dimension there is enough room to glue the edges together without creating intersections, and it is here where the glued square really exists.
    Tiling View: Life Inside the Klein Bottle Both the Klein bottle and torus satisfy the laws of Euclidean geometry from high school because we can tile the plane with a square without distortion- four 90 degree angles come together at a vertex to form 360 degrees. If we sketch what a creature living on the Klein bottle would see in all directions, this is called a tiling view. The top left is really just below the bottom right in this Klein Bottle universe because they are identified by the mirror reflection. However, if we look off to the right or left, we see exactly the same image instead of the reflected one.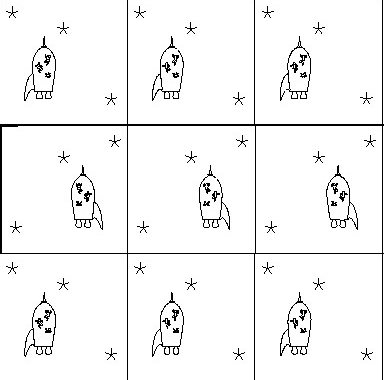
    Experience what it is like to live on a Klein Bottle by playing Klein Bottle Tic-Tac-Toe.
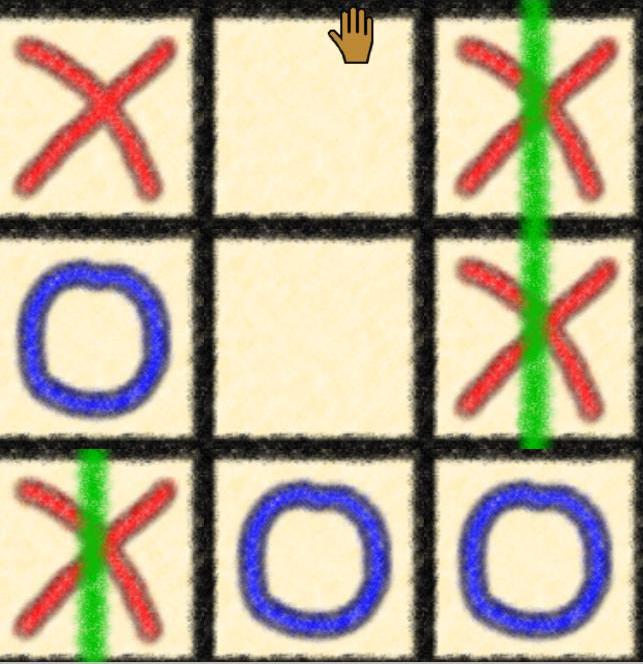
    * Choose a partner and have one person read these instructions while the other follows them.
    *Download Torus Games for Mac OS 10.12 or later. You can also download this free software onto other devices from the above link, if you prefer.
    * Select Tic-Tac-Toe.
    * Using the Options menu, change to Human vs. Human.
    * Using the Topology menu, change to Klein Bottle.
    * You are allowed to scroll the board by clicking on a grid line, holding down and moving. Move the hand that results to the right and see like it behaves like a Pac-Man. Move up to the top and see the reflection about the vertical purple dashed line. The esc key will let you access the menus or rest of your computer again.
    * The Rules: When the purple dotted line of reflection is in the middle, then the top left square is just below (out of view) the bottom right square in this Klein Bottle universe. The yellow dotted lines show the straight across identifications left to right, as you can see when you scroll horizontally.
    *Erase Tic-Tac-Toe Board will bring up a new game.

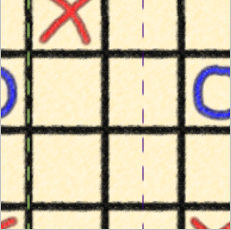
    A partially scrolled game showing the identifications


    Play on one computer with a partner:

  11. Winner where you scroll the board as you play to see the possibilities - best out of 3______________________

    Next scroll the board so that the purple dotted line of reflection is in the middle of the board. Then play without scrolling the board. It may help if you sketch a tiling view on a piece of paper as you make your moves, where left and right is the same as the board, but above and below are reflected (with the left and right columns swapped), like with the spaceship picture above.
  12. No Scrolling Winner - best out of 3______________________
    		13.


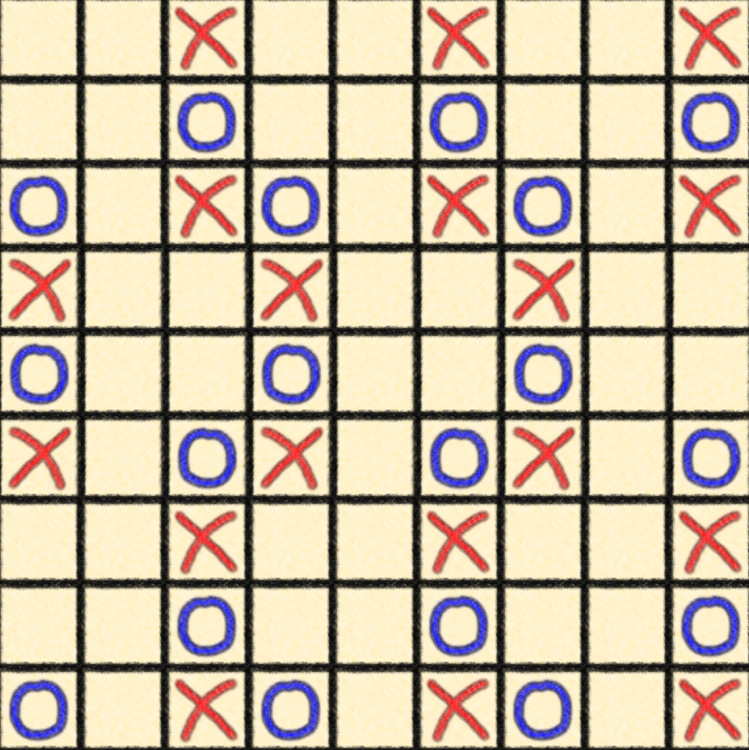    Play enough times of this, or another one of the games, that you understand the visualization of the Klein bottle tiling (reflected above and below, same image to the left and right - like the spaceships). The Klein bottle Pool Balls or the Maze are especially nice visualizations.

  13. Did you understand how to create a tiling view for a Klein bottle? If the answer is no, then play some more! ___________


  • Ask me any questions you have if there is time, and otherwise you may leave to work on homework.
    Dr. Sarah J. Greenwald, Appalachian State University