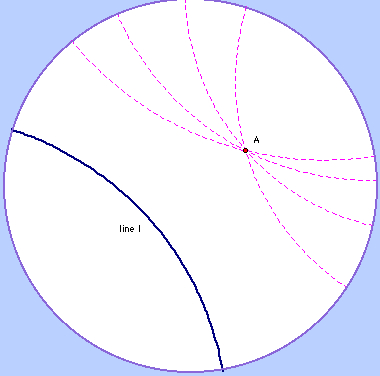
The following picture shows a model of hyperbolic geometry called the Poincare disk model. Imagine yourself at the center of the white disk and imagine this as a bowl that curves away from you. This visualization is not quite correct, but it will serve our purposes for now. The blue circle that encloses the disk is actually supposed to be infinitely far away from you. Hence, while this model looks like it is a flat disk, it really is not, and so the geometry is different too.
Given line l and point A not on l (as in the picture) it is possible to construct many lines that do not intersect l. In the picture we see four such (dashed) lines that are parallel to l. Hence Playfair's postulate is false in hyperbolic geometry. You might be concerned about that fact that these "lines" look more like curves. Yet in this geometry, these are shortest distance paths that are intrinsically straight (a stream of water would follow them as the path of least resistance), and so in this manner they are valid lines.
|
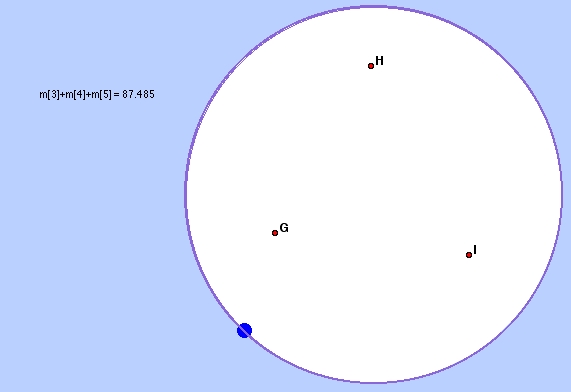
In this picture, We see three points, G, H and I.
To the left of the model, I've measured the sum of the
angles of the resulting hyperbolic triangle.
We see that this sum is 87.485 degrees!
The following file is an interactive version of the model accessible by clicking on this sheet from the lab directions web page. Drag the points H, G and I around to see what happens to the sum of the angles in the resulting hyperbolic triangle and then answer the following questions. Interactive Poincare disk angle sum |
|
Question 2 Move the points around (in the form of a triangle) so that the sum of the angles is as large as you can make it. How big is this number?
Question 3 Is your last triangle large or small? Explain why this makes sense by using the visualization of the model that is given in the intro.
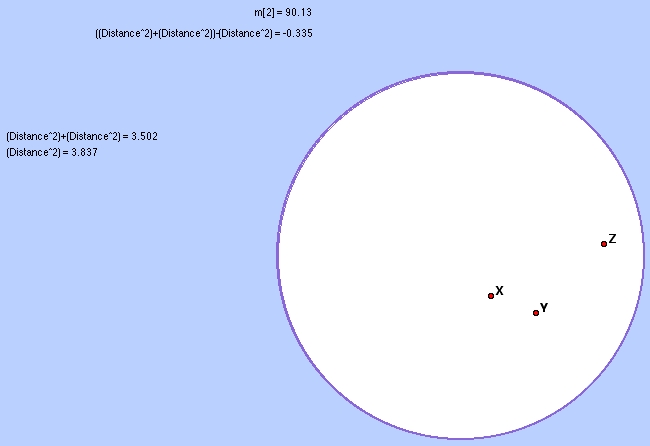
The following picture shows the Poincare disk model with three points X, Y and Z. I have measured angle XYZ and m[2] shows me that the measure of this angle is about 90 degrees. Hence XYZ forms a right triangle with XZ as the hypotenuse. I then calculated XY2 + YZ2 and compared it to XZ 2 to see whether the Pythagorean theorem holds in this model. We see that for this triangle XY2 + YZ2 - XZ2 = -.335 and so we see that XY2 + YZ2 < XZ2 by .335. Hence the Pythagorean theorem does not hold for this triangle in this model.
The following file is an interactive version of the model. Interactive Poincare Disk Pythagorean theorem
Question 1: Drag the points to make a small right triangle. Be sure that the points don't touch and be sure that the angle (m[2]) is as close to 90 degrees as you can make it without going under (ie make sure the angle is not 89.8 degrees).
Part a: What is the measure of the angle?
Part b: What is XY2 + YZ2 - XZ2 (which is listed as ((Distance^2)+(Distance^2))-(Distance^2)= ____)?
Question 2: Drag the points to make a large right triangle and be sure that the angle (m[2]) is close to 90 degrees without going under.
Part a: What is the measure of the angle?
Part b: What is XY2 + YZ2 - XZ2?
Question 3: Given this model, why does it make sense that for small right hyperbolic triangles the calculation XY2 + YZ2 - XZ2 is closer to 0 than is the same calculation for large right hyperbolic triangles?
In the weeks to come, we will see real-life applications of hyperbolic geometry.