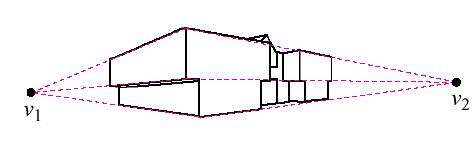
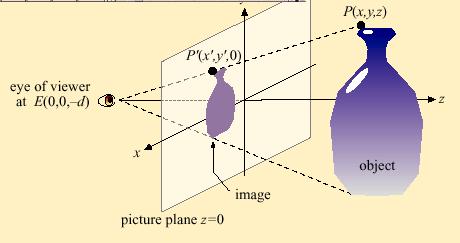
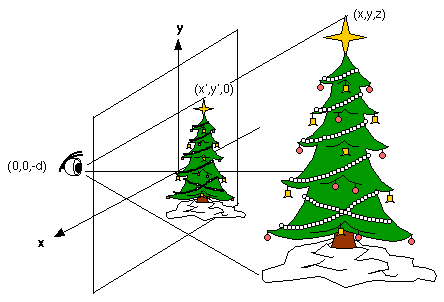
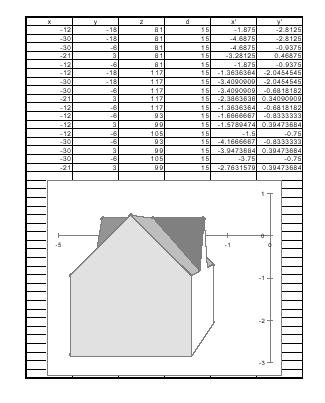
We use perspective drawing, or the rules of projective geometry, in order to accurately represent 3 dimensional space on a computer screen or piece of paper. Perspective drawing works because we can mathematically predict how our eyes (and brains) will see.

The use of perspective began during the Renaissance. It changed the way we represented and visualized the world.

We will now investigate some properties of perspective drawing and see how they can help us appreciate art and the world around us.

Adapted by Dr. Sarah from Marc Frantz's Mathematics and Art.

The idea of projective geometry (also known as perspective drawing) is to project a figure onto a plane. For example, we might look at a building outside of a window, and project what we see onto the window with masking tape.

Vanishing Points

Architectural lines that are parallel to one another in real-life, but not parallel to the plane of the window have images that converge to a common point in the drawing called a vanishing point. In projective geometry and in perspective drawing, lines that were parallel in the real-world now intersect. Hence, Playfair's postulate (given a line and a point off the line there exists a unique parallel to the line through the point) does not hold in projective geometry since we cannot find any parallels.

This is an especially effective use of perspective to show depth.

The correct use of vanishing points and other geometric devices can greatly enhance not only one's ability to draw realistically, but also one's ability to appreciate and enjoy art. The picture below shows 2 vanishing points v1 and v2 obtained from the perspective masking tape window drawing above.

Try to identify the vanishing point in the picture below. After you have done this, click on "Here is the answer!" to see the vanishing point (the point in the painting that lines parallel in the real world converge to).

Here is the answer!

Obtaining the Rules for Perspective Drawing

Experiments with perspective drawing were done long ago, when people with interdisciplinary interests (like math and art) were perhaps more common. In this 1525 woodcut, from "Unterweisung der Messung", by Albrecht Durer, the screw eye on the wall is the desired viewer's eye, the lute on the left is the object, the taught string is a light ray, and the picture plane is mounted on a swivel.

College art history professor Sam Edgerton believes that the discovery of the rules of perspective ushered in the industrial revolution. The newfound ability to reveal depth in drawings led to unprecedented sharing of ideas.

Using Mathematics to Create Precise Perspective Drawings

There are precise mathematical rules for perspective drawing and understanding just a little bit about these rules can help us view art more effectively.

A viewer's eye is located at the point E=(0,0,-d) in the (x,y,z) coordinate system located in 3-space (ie x=0, y=0, z=-d). Notice that just one eye is used. Out in the real world is an object, represented by a vase here. As light rays from points on the object (such as the point P(x,y,z) on the vase) travel in straight lines to the viewer's eye, they pierce the picture plane (the x-y plane where z=0), and we imagine them leaving behind appropriately colored dots, such as the point P'(x',y',0). The collection of all projection points P' comprise the perspective image (the perspective drawing) of the object. Take a look at the picture below and re-read this with this picture in mind.

Perspective Theorem

Given a point (x,y,z) of a real-life object with z > 0, the projections of these real-life 3D vase coordinates onto the 2D sheet (the perspective drawing coordinates) are given by the mathematical formulas.
x' = (d x) / (z+d)
y' = (d y) / (z+d)
where d is the distance from the viewer's eye at (0,0,-d) to the picture plane (z=0).
Hence, given a real-life 3-D object, the artist will draw x' and y' on their 2-D sheet.

I don't expect you to understand how these formulas were obtained, but I do expect you to know that these are formulas for the 2-D coordinates on the picture plane of the real-life object that will be drawn in correct perspective (see the picture above).

Example

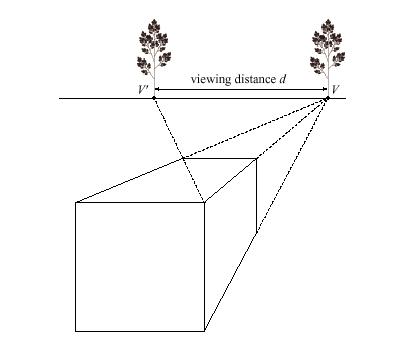
Suppose the viewer is 3 units from the picture plane. If P(2,4,5) is a point on an object we wish to paint, find the picture plane coordinates (x', y') of the perspective image of P.
Solution

We have d=3, x=2, y=4, z=5. Thus
x'=(d x) / (z+d) = (3*2)/(5+3)=6/8=3/4 and
y'=(d y) / (z+d) =(3*4)/(5+3)=12/8=3/2.

As a second example, we might want to make a perspective drawing of a real-life Christmas tree. We first put a dot at the image (x',y') of a point (x,y,z) where the coordinates of x' and y' are given by the perspective theorem as above. Then we continue to trace all possible such lines, accumulating all possible points P' associated with our original object. Once we have done this, we will end up with a perspective drawing of our Christmas tree.

Perspective Drawing in Excel

We are going to make a perspective drawing of a house in Excel using the above equations. Work in a group of 2. 1 person should read these directions to the 2nd person, while the 2nd person actually does this on their computer. You only need to do 1 Excel house per group. Click on this excel file from Internet Explorer. Your computer should automatically bring up Microsoft Excel, which is useful for amortization tables, calculations and spreadsheets.

You will see a chart that is partly filled in with real-life x, y and z coordinates of a house (in columns A, B and C, respectively). We will use the viewing distance of 15 (as in column D) to calculate x' and y', and create a perspective drawing of it in Excel. So, we want to mathematically project the three dimensional house onto the mathematically precise perspective image in the plane (where we can draw it).
So, we want to transform x, y and z to new coordinates x'=(d x)/(z+d) and y'=(d y) /(z+d). We will make Excel do these formulas for us!.

To transform x to x', click on E2 in the Excel sheet (row 2, column E). The Excel formula for x' that you should type in is:
=d2*a2/(c2+d2)
so type this formula (on the above line) into E2 and hit return. You should now see -1.875. Since d is in the d2 box, x is in the a2 box, and z is in the c2 box, we see that the Excel formula that we just typed in -
=d2*a2/(c2+d2)
is the correct formula to use in order to find the 2-D perspective coordinates of the given 3-D point, since it corresponds to the formula
x'=(d x)/(z+d)
Be sure that you understand this before moving on. Click on E2 again. At the bottom right corner of E2 scroll until you get a square with arrows which looks like

. Then click, hold down, and fill down the Excel column by scrolling down and releasing in E18. The number you will see there is -2.7631579.

To transform y', click on F2 in the Excel sheet. Figure out the Excel formula corresponding to y'=(d y)/(z+d) (hint - first make sure you understand the Excel formula that we used for x', and then figure out the corresponding Excel formula for y') and then type your Excel formula into F2 and hit return. You should now see -2.8125. At the bottom corner of F2 click until you get a square with arrows. Then fill down the Excel column and release in F18. The number you will see there is .39473684.

To draw our house, click on the grey E box, so that that column is highlighted. Then hold down the shift key while you click on the grey F box, so that both the E and F columns are now highlighted. Under Insert, release on Chart. Then click on XY (Scatter) and then on Finish. Now we have our mathematical drawing! All we have to do is connect the dots (see below)

Click on the blue or grey background part of your chart. Under View, scroll to toolbars, and then release on drawing. A "drawing toolbar" will appear. Click on the line that is just a straight line (no arrow heads or anything).
Your mouse should now be a thin cross when you take it to your picture.
We want to connect the dots to make the picture represented above.

Click on the bottom left point in the picture, hold down the mouse, and release on the point above it to draw the line representing the left side of the house. Then click on the blue part to complete the line.

Keep clicking on the line on the toolbar in order to draw lines on your picture in order to complete the picture as above.

To erase a line that you have drawn by mistake, click on the arrow in the drawing tools, and then go back to the picture. Hold the mouse over the line until it turns into a hand. Wait until it tells you Line (--) where (--) means some number. Then click down, and hit delete.

Dr. Sarah will show you how to use the dots to make lines that are not formed directly by connecting 2 dots (the line coming down from the top left of the roof and the little line from the top right of the base of the house connecting to the roof) First you make a complete line down to the corresponding dot, then make a line to the part that you desired, and then erase the longer line.

Show Dr. Sarah your completed house.

One-Point Perspective and Viewing Distance

The following box has one vanishing point, but it also satisfies an additional condition -- lines in the sketch which converge to V represent lines in the real world which are perpendicular to the picture plane. A painting which satisfies these two conditions is said to be in one-point perspective.

When a picture is in true one-point perspective, there is an optimal viewing distance d from which we should step back and view it from the vanishing point V. As we see in the vase and Christmas tree drawings above, the rules of perspective assume that the viewer has one eye open and is viewing the work of art from a distance d. The idea is that the drawing follows mathematically precise rules, and that if we close one eye and step back a distance d from V, then we will appreciate the 3-D aspect better.

So, we want to locate the viewing distance d. The way we do this is as follows:

We first locate the vanishing point V that parallel lines directly in front of us converge to.

We then draw a horizontal line through V.

We find a rectangular feature that is on the same horizon (the same height) as the horizontal line through V and has some lines converging to V.

We then trace one of the diagonals of this rectangular feature. We look at the intersection of this diagonal line with the horizontal line from V, and call this intersection V'.

We measure the distance from V to V' which is equal to d.

In the drawing of the box below, in order to locate d, we locate V' by drawing the dashed diagonal line of the top face of the box. How do we know that V' is on the same horizontal line as V? Because the dashed lines are images of real lines which are level with the ground, so the sight lines of the viewer to their vanishing points must be level also.

Recall that the reason that we want to determine d is that the picture was drawn assuming that it would be viewed with one eye from a distance d behind V, and so this is the optimal viewing place and distance. To test out our determination of d,

click on this link of the large drawing and do as follows as you have a partner read you these directions:

Close your right eye.

Place your left eye directly in front of the point V (NOT in the center of the page!). You will need to get very close to the computer screen to do this.

Use a thumb and a forefinger to measure the distance between V and V' which you should see as 2 dots at the very top of your screen.

Use this to measure out d units in front of V. Move until your left eye is exactly d units away from V on the computer screen. You will still be very close to the computer screen!

Without changing your position, let your eye roll down and to the left and then look at the box. Although it may be too close for comfortable viewing because you will be so close to the computer screen, the distortion should go away and it should look much more like a cube! Most people will be able to see this by following the directions, but some people may have problems due to glasses, ...

Now switch roles and read the directions to your partner as they complete this activity.

We have only used a little mathematics, but we have accomplished a lot. We have seen the importance of the unique, correct perspective viewpoint. If we view art from the wrong viewpoint, it can appear distorted -- a cube can look like a dumpster. If we view art from the correct viewpoint, it will give us the true perspective desired by the artist. In addition, the majority of perspective works in museums are done in one-point perspective, with clues that can help determine the viewing distance. Thus our simple trick can actually be used in viewing and enjoying many paintings in museums and galleries.

Calculating the Viewing Distance for Interior of Antwerp Cathedral, by Peter Neeffs the Elder, 1651

In the figure below, we see the trick applied to finding the viewpoint for the Interior of Antwerp Cathedral painting. We first determine the vanishing point V directly in front of us, which is easy to see, as it is the intersection of lines which are supposed to be parallel in the real-world. Some of the lines have been drawn in below in order to highlight V. Notice that lines that follow along the edges (coming from us towards V) of the square tiles of the floor also intersect at V. Since the floor tiles are squares, they serve the same purpose as the square top of the cube in the previous discussion. Hence, our second point V' is calculated by following along a diagonal (indicated on the picture) that follows along the vertices of the square tiles. If we had chosen the diagonals of other square tiles, we still would have converged to V', or to a point V'' on the other side of V that is also d units away from V. In either case, the viewing distance d is the indicated length, and the correct viewpoint is directly in front of the main vanishing point V.

Although it is not possible to tell by viewing this small reproduction of Interior of Antwerp Cathedral, the effect of viewing the actual painting in the Indianapolis Museum of Art gives a surprising sensation of depth, of being "in" the cathedral. The viewing distance is only about 24 inches, so most viewers never view the painting from the best spot for the sensation of depth!

Of course you can't draw lines on the paintings and walls of an art museum, so some other method is needed to find the main vanishing point and the viewing distance. A good solution is to hold up a pair of wooden shish kebab skewers, aligning them with lines in the painting to find the location of their intersection points. First, the main vanishing point V is located. Then one skewer is held horizontally so that it appears to go through V, and the other is held aligned with one of the diagonals of the square tiles; the intersection point of the skewers is then V'. The figures below show people using their skewers to determine the viewpoint of a perspective painting. Then, one by one, the viewers assume the correct viewpoint, looking with one eye to enjoy the full perspective effect. If shish kebab skewers aren't practical, any pair of straight edges, such as credit cards, will work almost as well for discovering viewpoints of perspective works.

Of course there are other important ways to view a painting. It's good to get very close to examine brushwork, glazes, and fine details. It's also good to get far away to see how the artist arranged colors, balanced lights and darks, etc. Our viewpoint-finding techniques add one more way to appreciate, understand, and enjoy many wonderful works of art.

Extra Credit Find a real-life painting that was done in one-point perspective and adapt the method to find the viewing distance of this painting. Write up a report on how you did this, giving specific details, and also discuss what you saw when you used the proper viewing distance for your painting. I recommend that you re-read the reading above before you try this.