The use of perspective began during the Renaissance. It changed the way we represented and visualized the world.
We will now investigate some of the mathematical properties of perspective drawing and see how they can help us appreciate art and the world around us.
Experiments with perspective drawing were completed long ago,
when people with interdisciplinary interests (like mathematics
and art) were
perhaps more common. In this 1525 woodcut,
from "Unterweisung der Messung", by Albrecht Durer,
the screw eye on the wall is
the desired viewer's eye, the lute on the left is the object,
the taught string is a light ray, and the picture plane is mounted on
a swivel.
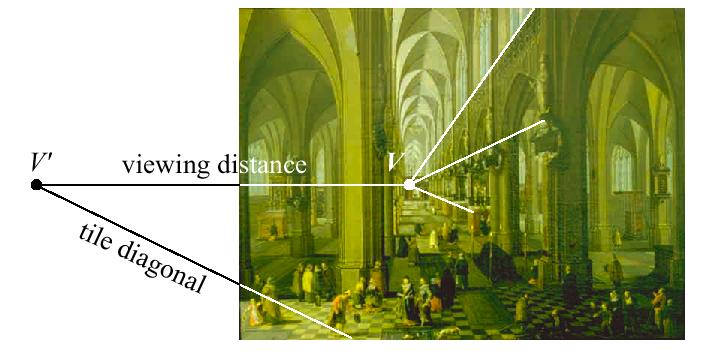
Calculating the Viewing Distance for Interior of Antwerp Cathedral, by Peter Neeffs the Elder, 1651
In the figure below, we see the trick applied to finding the viewpoint for the Interior of Antwerp Cathedral painting by Peter Neeffs the Elder. We first determine the vanishing point V directly in front of us, which is easy to see, as it is the intersection of lines which are supposed to be parallel in the real-world. Some of the lines have been drawn in below in order to highlight V. Notice that lines that follow along the edges (coming from us towards V) of the square tiles of the floor also intersect at V, in the picture below. Our second point V' is calculated by following along a diagonal (indicated on the picture) that follows along the vertices of the square tiles. The viewing distance d is the indicated length, and the correct viewpoint is directly in front of the main vanishing point V.Although it is not possible to tell by viewing this small reproduction of Interior of Antwerp Cathedral, the effect of viewing the actual painting in the Indianapolis Museum of Art gives a surprising sensation of depth, of being "in" the cathedral. The viewing distance is only about 24 inches, so most viewers never view the painting from the best spot for the sensation of depth!
Activity 1: Come One - Come All - to a Better Cube
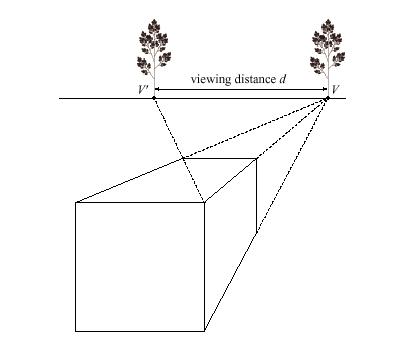
This picture was drawn assuming that it would be viewed with one eye from a distance d behind V. Click on this link of the large drawing and do as follows as you have a partner read you these directions:
- Use a thumb and a forefinger to measure the distance d between V and V' which you should see as 2 dots at the very top of your screen. Keep this distance with your hand.
- Continuing to keep that distance, turn your hand 90 degrees (perpendicular to the screen) to measure out d units in front of V.
- Place your left eye exactly at that same point (d units in front of V - not in the center of the page). You will need to get very close to the computer screen to do this.
- Close your right eye.
- Without changing your position, let your left eye roll down and to the left and then look at the box. Although it may be too close for comfortable viewing because you will be so close to the computer screen, the distortion should go away and it should look much more like a cube! Most people will be able to see this by following the directions, but some people may have problems due to astigmatism...
- Now switch roles and read the directions to your partner as they complete this activity.
If we view art from the wrong viewpoint, it can appear distorted -- a cube can look like a dumpster. If we view art from the correct viewpoint, it will give us the true perspective desired by the artist. In addition, the majority of perspective works in museums are done in one-point perspective, with clues that can help determine the viewing distance. Thus our simple trick can actually be used in viewing and enjoying many paintings in museums and galleries. Viewers in a gallery or museum almost never assume the correct perspective viewpoint, because these locations tend to be rather low, off-center, rather close, etc. It's true that the artwork may appear perfectly acceptable from most locations in the room. However, when one assumes the correct viewpoint and looks with one eye, it is common for the illusion of depth to be astonishingly more believable. You can almost "feel" the space! (Of course the work must be of high quality and very precise.) While you can't draw dashed lines on the artwork to find the viewing distance, you can mentally trace appropriate lines by holding up shish kebab skewers. Once you do so, you can use your hands to measure the viewing distance in the painting and stand d units in front of V.
Using Mathematics to Create Precise Perspective Drawings and Computer Animations
Mathematicians and artists found the precise mathematical rules for perspective drawing. Understanding just a little bit about these rules can help us understand art and computer animation.A viewer's eye is located at the point E=(0,0,-d) in the (x,y,z) coordinate system located in 3-space (ie x=0, y=0, z=-d). Notice that just one eye is used, like in the cube example. Out in the real world is an object, represented by a vase here. As light rays from points on the object (such as the point P(x,y,z) on the vase) travel in straight lines to the viewer's eye, they pierce the picture plane (the x-y plane where z=0), and we imagine them leaving behind appropriately colored dots, such as the point P'(x',y',0). The collection of all projection points P' comprise the perspective image (the perspective drawing) of the object.
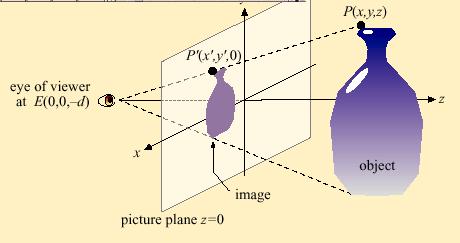
Perspective Theorem
Given a point (x,y,z) of a real-life object with z > 0, the projections of these real-life 3D vase coordinates onto the 2D sheet (the perspective drawing coordinates) are given by the mathematical formulas.x' = (d x) / (z+d)
y' = (d y) / (z+d)
where d is the distance from the viewer's eye at (0,0,-d) to the picture plane (z=0).
Hence, given a real-life 3-D object, the artist will draw x' and y' on their 2-D sheet.
Example
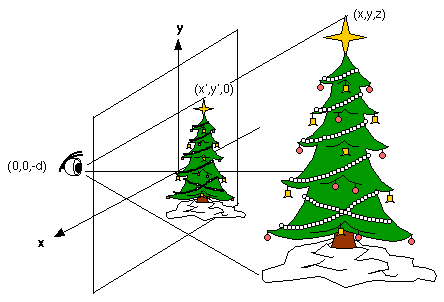
Suppose the viewer is 3 units from the picture plane. If P(2,4,5) is a point on an object we wish to paint, find the picture plane coordinates (x', y') of the perspective image of P.As a second example, we might want to make a perspective drawing of a real-life Christmas tree. We first put a dot at the image (x',y') of a point (x,y,z) where the coordinates of x' and y' are given by the perspective theorem as above. Then we continue to trace all possible such lines, accumulating all possible points P' associated with our original object. Once we have done this, we will end up with a perspective drawing of our Christmas tree.Solution
We have d=3, x=2, y=4, z=5. Thus
x'=(d x) / (z+d) = (3*2)/(5+3)=6/8=3/4 and
y'=(d y) / (z+d) =(3*4)/(5+3)=12/8=3/2.
Activity 2: Perspective Drawings on a Computer
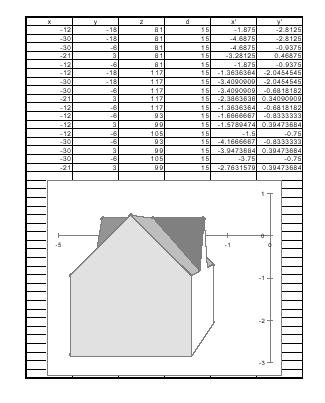
We are going to make the computer create a perspective drawing of a house by using the above equations. Work with a partner - have one person read the directions on their screen while the other performs the instructions.Download and open this Excel file using the program with the green X. You will see a chart that is partly filled in with real-life x, y and z coordinates of a house (in columns A, B and C, respectively). We will use the viewing distance of 15 (as in column D) to calculate x' and y', and create a perspective drawing of it in Excel. So, we want to mathematically project the three dimensional house onto the mathematically precise perspective image in the plane (where we can draw it).
So, we want to transform x, y and z to new coordinates x'=(d x)/(z+d) and y'=(d y) /(z+d). We will make Excel do these formulas for us!
.
Then click, hold down, and
fill down the Excel column by scrolling down and releasing in E18. The number
you will see there is -2.7631579.
use many more rows of Excel. The full-body version of
this Yoda uses 53,756 vertices!
