1. If a linear system is inconsistent then
    a) at least 2 of the lines or planes are parallel
    b) we are missing a pivot for some x_i
    c) some row in the reduced augmented matrix is [0 0 ... 0 nonzero]
    d) more than one of the above
    e) none of the above



  2. What is the solution to the system of equations represented with this reduced augmented matrix?
    1 0 0 2
    0 1 0 3
    0 0 1 4


    a) (2,3,4)
    b) (1,1,1)
    c) There are an infinite number of solutions
    d) There are no solutions
    e) We can't tell without having the system of equations



  3. How many solutions to a linear system of equations are possible?
    a) 0 or 1
    b) 0, 1, or 2
    c) 0, 1, 2 or infinite
    d) 0, 1, infinite
    e) any number of solutions is possible
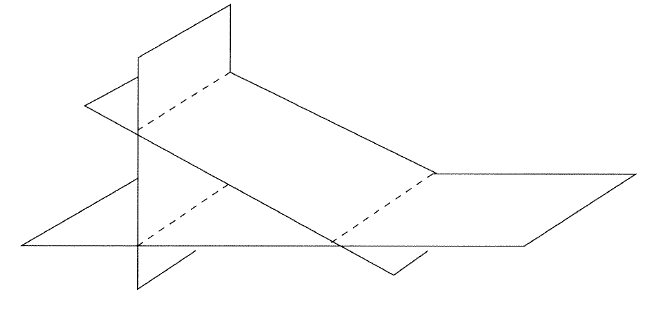
  4. According to the language of linear algebra, this picture
    a)lies inside of R2, the x-y plane.
    b)shows 3 linear equations that have 3 lines as the solutions
    c)shows that 3 non-parallel planes do not have to have any points in common
    d)more than one of the above choices are possible



  5. How can we geometrically represent the parametric equations (2t, -t + 1, t)?
    a) A line in R2
    b) A line in R3
    c) A plane in R3
    d) A volume in R3



  6. We find that a system of three linear equations in three variables has an infinite number of solutions. What would guarantee that this would happen?

    a) We have three equations for the same plane.
    b) At least two of the equations represent the same plane.
    c) The three planes intersect along a line.
    d) The planes represented are parallel.
    e) More than one of the above choices are possible.


  7. I am feeling comfortable with the by-hand method of Gaussian/Echelon form with row reductions being used to to obtains 0s below the diagonal:
    a) Definitely
    b) Somewhat
    c) Unsure
    d) Somewhat not
    e) What are row reductions?


  8. Use Gaussian on the following augmented matrix:
    1 1 0 2
    2 1 3 3
    2 2 h 4
    Which of the following are true?
    a) it takes at least 3 elementary row operations to get to Gaussian here
    b) from Gaussian we can see that we have full pivots for all h
    c) from Gaussian we can see that some h give us no solutions
    d) more than one of the above is true
    e) none of the above



  9. For full credit, which of the following are true regarding graded problem sets:
    a) I am only allowed to use the book, my group members, the math lab and Dr. Sarah for help on the problem set.
    b) I can use any source for help, but the work and explanations must be distinguished as originating from my own group and I must acknowledge any help outside the group or Dr. Sarah, like "the idea for problem 1 came from discussions with johnny or this website..."



  10. For full credit, which of the following are true regarding graded problem sets
    a) I must print out all work, including Maple ReducedRowEchelonForm commands and output
    b) I must annotate/explain my methods and reasoning with handwritten comments and/or typed comments.
    c) both a) and b)
    d) neither a) nor b)



  11. For full credit, which of the following are true regarding True/False questions?
    a) For a false statement I should try and quote the book and explain
    b) For a false statement I should try and provide one counterexample that violates the statement
    c) both a) and b)
    d) neither a) nor b)