Bioinformatics and Linear Algebra: Amanda Jones
Conway's Game of Life: Joe
Cramer's Rule: Ashley Carrigan
Cryptography: Yeoly Ly
Cryptography and Matrices: Katie Farmer and Meagen McAndrews
Diagonalization of inertial tensors to find the principle axes: Kevin Holway and Luke
Eight Queens and Determinants: Robert Bost and Kelly
Eigenfaces and Facial Recognition: Jeremy Coleman
Hill Ciphers and Linear Algebra: Cayley Strub
Images in Java: Shawn
Lights Out: Brett Coleman
Linear Algebra in High School: Megan Ames
Linear Algebra in High School: Josh Prince
Thermal Profiles of an Urbanized Stream and Matrices: Rachel
Networks: Tim Gallagher
Rubik's Cube and Matrices: Ryan Belt
Shear Matrix Applications: Katie Owens and Miranda Neaves
Note: You may work with two other people and turn in one per group of three
Hints and Commands for Problem Set 6
Problem 1: 7.1 #14 by hand and on Maple via the Eigenvectors(A); command also compare your answers and resolve any apparent conflicts or differences.
Problem 2: Rotation matrices in R2 Recall that the general rotation matrix which rotates vectors in the counterclockwise direction by angle theta is given by
M:=Matrix([[cos(theta),-sin(theta)],[sin(theta),cos(theta)]]);
Part A: Apply the Eigenvalues(M); command. Notice that there are real eigenvalues for certain values of theta only. What are these values of theta and what eigenvalues do they produce? (Recall that I = the square root of negative one does not exist as a real number and that cos(theta) is less than or equal to 1 always.)
Part B: Find a basis for the corresponding eigenspaces.
Part C: Use only a geometric explanation to explain why most rotation matrices have no eigenvalues or eigenvectors (ie scaling along the same line through the origin).
Problem 3: 7.2 7
Problem 4: 7.2 18
Problem 5: 7.2 24
Problem 6: Foxes and Rabbits (Predator-prey model)
Suppose a system of foxes and rabbits is given as:
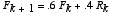
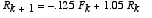
Part A: Write out the Eigenvector decomposition of the iterate xk, where the foxes Fk are the first component of this state vector, and the rabbits Rk the second.
Part B: Use the decomposition to explore what will happen to the vector xk in the longterm, and what kind of vector(s) it will travel along to achieve that longterm behavior, and then fill in the blanks:
If ___ equals 0 then we die off along the line____ [corresponding to the eigenvector____], and otherwise we [choose one: die off or grow or hit and then stayed fixed] along the line____ [corresponding to the the eigenvector____].
Part C: Determine a value to replace 1.05 in the original system that leads to constant levels of the fox and rabbit populations (ie an eigenvalue of 1), so that eventually neither population is changing. What is the ratio of the sizes of the populations in this case?
1) Skim 7.1 to find the definition for an eigenvalue and an eigenvector and write it down.
2) Research the web for information about eigenvectors and write down a few items that you found interesting.
Note: You may work with two other people and turn in one per group.
Hints and Commands for PS 5
Problem 1: 4.4 16
Problem 2: 4.5 24
Problem 3: 4.5 48
Problem 4: Cement Mixing Continued (**ALL IN MAPLE**) This problem is worth more than the others
Problem 5: 4.6 24
Problem 6: 4.6 27
4.4 11, 53
4.5 22
Hints and Commands for Problem Set 4
Problems 1: 4.1 36
Problem 2: 4.1 44
Problem 3: Cement Mixing (*ALL IN MAPLE*) *This problem is worth more than the others.
Problem 4: 4.2 22
Problem 5: Natural Numbers Prove that the natural numbers (scalar multiplication as usual) is not a vector space using axiom 6.
Problem 6: True or False: The line x+y=0 is a vector space.
Problem 7: Solutions to the plane 2x-3y+4z=5, ie {(x,y,z) in R^3 so that 2x-3y+4z=5} Prove that this is not a subspace of R3 using axiom 1 (addition as usual).
Problem 8: 4.3 (14 part D - Be sure to leave n as general as in class - do not define it as 2x2 matrix). Prove that this is not a subspace (addition as usual).
4.1 35, 43, 52
4.2 21 [Show that axiom 1 is violated, ie find two determinant 0 matrices that sum to a matrix with determinant non-zero]
4.1 7 and 49.
Note: You may work with at most two other people and turn in one per group.
Maple Commands and Hints for PS 3 I also encourage you to ask me questions about anything you don't understand in office hours or message me on ASULearn. Your group's explanations must distinguish your work as your own.
Problem 1: 2.5 24
Problem 2: Healthy/Sick Workers (all on Maple including text comments) *This problem is worth more than the others.
Problem 3: 3.1 47 part a
Problem 4: 3.2 32 part c
Problem 5: 3.3 (28 by-hand and on Maple)
Problem 6: 3.3 (34 if a unique solution to Sx=b exists, find it by using the method x=MatrixInverse(S).b in Maple).
Problem 7: 3.3 (50 parts a & c)
Part A Set up the stochastic matrix N for the system. The first column of N represents A->A, A->B, and A->Neither [.75, .20, .05 is the first column; .75, .15, .10 is the first row].
Part B Using regularity, we can see that the system will stabilize since the columns add to 1, and the entries are all positive. Find the steady-state vector by setting up and solving (N-I)x=0 for x. Recall that if you add a row of 1s at the bottom, this will solve for the value you want [the entries add to 100%].
Note: You may work with at most two other people and turn in one per group.
Maple Commands and Hints for PS 2 I also encourage you to ask me questions about anything you don't understand in office hours or message me on ASULearn. Your group's explanations must distinguish your work as your own.
Problem 1: 2.1 30
Problem 2: 2.2 34 parts a, b & c
Problem 3: Show that the following statements about matrices are false by producing counterexamples and showing work:
Statement a) A2=0 implies that A = 0
Statement b) A2=I implies that A=I or A=-I
Statement c) A2 has entries that are all greater than or equal to 0.
Problem 4: 2.3 12
Problem 5: 2.3 14 by hand and on Maple
Problem 6: 2.3 28 part a - look at the matrix system as Ax=b and then apply the inverse method of solution
Problem 7: 2.3 40 part d
2.1 (by-hand: 9, 32)
2.2 (by-hand: 17, 18), (35 parts b and c)
Note: You may work with at most two other people and turn in one per group.
Problem Set 1 Maple Commands and Hints. I also encourage you to ask me questions about anything you don't understand in office hours or message me on ASULearn. Your group's explanations must distinguish your work as your own.
Problem 1: 1.1 60 part c
Problem 2: 1.1 74
Problem 3: 1.2 30 by hand and also on Maple
Problem 4: 1.2 32
Problem 5: 1.2 44 parts a) through d) - in b) and d) find all the values of k and justify
Problem 6: 1.3 24 parts a and b
Problem 7: 1.3 26
1.2 25, 27, and (43 - find all the values of k and justify why these are all of them). Do not worry about getting the same answer as the back of the book (although it would be nice!) but do concentrate instead on making sure you understand the method of Gaussian Elimination.
1.1 7, 15, 19, (59 parts b and c), and 73.
Don't worry about getting the correct answer - instead concentrate on the ideas and the methods. This will count as participation and will not receive a specific grade, although I will mark whether you attemped the problems. For true/false questions, if a part is false, provide a specific counterexample, if it is true, quote a phrase from the text.