Note: You may work with one other person and turn in one per group of two but each person must complete and turn in Problem 1 themselves (in their own words).
Problem 1: 7.1 #14 by hand and on Maple via the Eigenvectors(A); command also compare your answers and resolve any apparent conflicts or differences within Maple text comments.
Problem 2: Rotation matrices in R2 Recall that the general rotation matrix which rotates vectors in the counterclockwise direction by angle theta is given by
M:=Matrix([[cos(theta),-sin(theta)],[sin(theta),cos(theta)]]);
Part A: Apply the Eigenvalues(M); command. Notice that there are real eigenvalues for certain values of theta only. What are these values of theta and what eigenvalues do they produce? Also find a basis for the corresponding eigenspaces. (Recall that I = the square root of negative one does not exist as a real number and that cos(theta) is less than or equal to 1 always.)
Part B: Use only a geometric explanation to explain why most rotation matrices have no eigenvalues or eigenvectors.
Problem 3-5: 7.2 7, 18, and 24
Problem 6: Foxes and Rabbits (Predator-prey model)
Suppose a system of foxes and rabbits is given as:
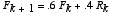
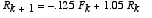
Part A: Write out the Eigenvector decomposition of the iterate x_k, where the foxes F_k are the first component of this state vector, and the rabbits R_k the second.
Part B: Use the decomposition to explain what will happen to the vector x_k in the longterm, and what kind of vector(s) it will travel along to achieve that longterm behavior.
Extra Credit: Determine a value of the [2, 2] entry that leads to constant levels of the fox and rabbit populations, so that eventually neither population is changing. What is the ratio of the sizes of the populations in this case?
Note: You may work with one other person and turn in one per group.
Problem 1: 4.4 16
Problems 2-3: 4.5 24, 48
Problem 4: Cement Mixing Continued (**ALL IN MAPLE**) This problem is worth more than the others
Problems 5-6: 4.6 24, 27
4.4 11, 53
4.5 22
Note: You may work with one other person and turn in one per group.
Problem 3: Cement Mixing (*ALL IN MAPLE*) *This problem is worth more than the others.
Problems 4-7: For all of the following vector space and subspace problems: If it is a vector space or subspace, then just state that it is, but if it is not, then write out the complete proof that one axiom is violated as in class:
4.2 22
Natural Numbers Prove that the natural numbers is not a vector space using axiom 6.
True or False: The line x+y=0 is a vector space.
Solutions to 2x-3y+4z=5, ie {(x,y,z) in R^3 so that 2x-3y+4z=5} Prove that this is not a subspace of R3 using axiom 1.
Problem 8: 4.3 (14 part D be sure to leave n as general - do not define it as 2)
4.1 7, 35, 43, 49, 52,
4.2 21
Note: You may work with one other person and turn in one per group of two
Problem 1: 2.5 24
Problem 2: Healthy/Sick Workers (all on Maple) *This problem is worth more than the others.
Problem 3: 3.1 47 a
Problem 4: 3.2 32 c
Problem 5-7: 3.3 (28 by-hand and on Maple), (34 if a unique solution to Sx=b exists, find it by using the method x=S^(-1) b), and (50 a and c)
2.5 10 set-up the stochastic matrix and calculate month 1 only.
3.1 33 by-hand using the co-factor expansion method.
3.2 25 by-hand using some combination of row operations and the co-factor exapansion method.
3.3 31
Note: You may work with one other person and turn in one per group of two but each person must complete and turn in Problem 5 themselves (in their own words).
Problem 1: 2.1 30
Problem 2: 2.2 (34 parts a, b and c)
Problem 3: Show that the following statements about matrices are false by producing counterexamples and showing work:
Statement a) A2=0 implies that A = 0
Statement b) A2=I implies that A=I or A=-I
Statement c) A2 has entries that are all greater than or equal to 0.
Problems 4-7: 2.3 12, (14 by hand and on Maple), (28 part a - look at the matrix system as Ax=b and then apply the inverse method of solution), and (40 part d)
2.1 (7 use matrix algebra and equality to obtain a system of 4 equations in the 3 unknowns and then solve), (by-hand: 9, 11, 15, 32)
2.2 17, 18, (35 use matrix algebra to combine the elements, set it equal to the other side, use matrix equality to obtain equations, and solve.)
Note: You may work with one other person and turn in one per group of two but each person must complete and turn in Problem 3 themselves (in their own words).
Problems 1-2: 1.1 60 b and c, 74,
Problems 3-5: 1.2 (30 by hand and also on Maple), 32, (44 find all values of k and justify),
Problems 6-7: 1.3 24 a and b, 26
1.2 15, 25, 27, (43 find all the values of k and justify why these are all of them), and 49. Do not worry about getting the same answer as the back of the book (although it would be nice!) but do concentrate instead on making sure you understand the method of Gaussian Elimination.
1.1 7, 15, 19, (59 parts b and c - if it is false, provide a counterexample), and 73.