Applications of Linear Algebra to Electron Microscopy: Zach Russell
Chemistry and Linear Algebra: Benjamin Deming
Computer graphics program which models the movement of the solar system. All calculations (rotations, transformations, scaling, etc...) will be based off of linear algebra calculations in a 3D environment: Jared Beckerman
Coding and Satellite Encryption and Linear Algebra: Dewey Bustle and Michael Huey
Cryptology and Linear Algebra: Dustin King
Contra Dancing and Matrices: Graylyn Byrd
Fractals and Linear Algebra: Robert McKinnon and Rachel Sigmon
Game Theory, Linear Algebra, and Tic Tac Toe: Lateef Livers and Arthur Wofford
Gaussian Elimination in Java: Hung Pham and Bobby Tokajer
Genetically Inherited Traits and Diseases: Lianna Beard
Genetic Algorithms: Aaron Folstad
Gershgorin Circle Theorem and Applications to Flutter of an Aircraft: David O'Connor
History of Linear Algebra: Mandi McGaha and Kimberly Eckard
Linear Programming: Ben Thompson
Matrix Applications in Optics: Ashley Roberts
NFL Rates the Passing Ability of Quarterbacks: Chris Depenbrock
Robotics, Matrices, and Linear Algebra: Jessie Goodrum and Terry Jordan
The use of Linear Algebra in search engines on the web: Jonathan Hearing
Note: You may work with two other people and turn in one per group of three
Problem 1: 7.1 #14 by hand and on Maple via the Eigenvectors(A); command also compare your answers and resolve any apparent conflicts or differences within Maple text comments.
Problem 2: Rotation matrices in R2 Recall that the general rotation matrix which rotates vectors in the counterclockwise direction by angle theta is given by
M:=Matrix([[cos(theta),-sin(theta)],[sin(theta),cos(theta)]]);
Part A: Apply the Eigenvalues(M); command. Notice that there are real eigenvalues for certain values of theta only. What are these values of theta and what eigenvalues do they produce? Also find a basis for the corresponding eigenspaces. (Recall that I = the square root of negative one does not exist as a real number and that cos(theta) is less than or equal to 1 always.)
Part B: Use only a geometric explanation to explain why most rotation matrices have no eigenvalues or eigenvectors.
Problem 3-5: 7.2 7, 18, and 24
Problem 6: Foxes and Rabbits (Predator-prey model)
Suppose a system of foxes and rabbits is given as:
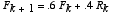
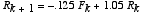
Part A: Write out the Eigenvector decomposition of the iterate xk, where the foxes Fk are the first component of this state vector, and the rabbits Rk the second.
Part B: Use the decomposition to explain what will happen to the vector xk in the longterm, and what kind of vector(s) it will travel along to achieve that longterm behavior.
Part C: Determine a value to replace 1.05 in the original system that leads to constant levels of the fox and rabbit populations (ie an eigenvalue of 1), so that eventually neither population is changing. What is the ratio of the sizes of the populations in this case?
Note: You may work with two other people and turn in one per group.
Hints and Commands for PS 5
Problem 1: 4.4 16
Problems 2-3: 4.5 24, 48
Problem 4: Cement Mixing Continued (**ALL IN MAPLE**) This problem is worth more than the others
Problems 5-6: 4.6 24, 27
4.4 11, 53
4.5 22
Problem 2 of the group work
Note: You may work with two other people and turn in one per group.
Hints and Commands for Problem Set 4
Problems 1-2: 4.1 36 and 44
Problem 3: Cement Mixing (*ALL IN MAPLE*) *This problem is worth more than the others.
Problems 4-7: For all of the following vector space and subspace problems: If it is a vector space or subspace, then just state that it is, but if it is not, then write out the complete proof that one axiom is violated as in class:
4.2 22
Natural Numbers Prove that the natural numbers is not a vector space using axiom 6.
True or False: The line x+y=0 is a vector space.
Solutions to the plane 2x-3y+4z=5, ie {(x,y,z) in R^3 so that 2x-3y+4z=5} Prove that this is not a subspace of R3 using axiom 1.
Problem 8: 4.3 (14 part D be sure to leave n as general as in class - do not define it as 2x2)
4.2 21
4.1 7, 35, 43, 49, 52
Note: You may work with at most two other people and turn in one per group.
Maple Commands and Hints for PS 3
Problem 1: 2.5 24
Problem 2: Healthy/Sick Workers (all on Maple including text comments) *This problem is worth more than the others.
Problem 3: 3.1 47 part a
Problem 4: 3.2 32 part c
Problem 5: 3.3 (28 by-hand and on Maple)
Problem 6: 3.3 (34 if a unique solution to Sx=b exists, find it by using the method x=S^(-1) b)
Problem 7: 3.3 (50 parts a & c)
2.5 number 10. We set this up in class and saw that the first column of N represented A->A, A->B, and A->Neither [.75, .20, .05 is the first column; .75, .15, .10 is the first row]. Using regularity, we can see that the system will stabilize since the columns add to 1, and the entries are all positive. Find the steady-state vector by solving (N-I)x=0 for x.
3.1 33 by-hand using the co-factor expansion method. Expand along the first column to take advantage of the 0s, and then the 1st column of the next 4x4 matrix, and then the 3rd row of the 3x3 matrix.
3.2 25 by-hand using some combination of row operations and the co-factor exapansion method.
3.3 31
Maple Commands and Hints for PS 2
Note: You may work with at most two other people and turn in one per group but each person must complete and turn in Problem 5 themselves (in their own words).
Problem 1: 2.1 30
Problem 2: 2.2 (34 parts a, b & c)
Problem 3: Show that the following statements about matrices are false by producing counterexamples and showing work:
Statement a) A2=0 implies that A = 0
Statement b) A2=I implies that A=I or A=-I
Statement c) A2 has entries that are all greater than or equal to 0.
Problems 4-7: 2.3 12, (14 by hand and on Maple), (28 part a - look at the matrix system as Ax=b and then apply the inverse method of solution), and (40 part d)
2.1 (by-hand: 9, 32)
2.2 (by-hand: 17, 18), (35 use matrix algebra to combine the elements, set it equal to the other side, use matrix equality to obtain equations, and solve using the ReducedRowEchelonForm command on Maple. No need to print out your Maple work - just summarize it on your homework.)
Note: You may work with at most two other people and turn in one per group but each person must complete and turn in Problem 3 themselves (in their own words).
Problems 1-2: 1.1 60 b and c, 74,
Problems 3-5: 1.2 (30 by hand and also on Maple), 32, (44 find all values of k and justify),
Problems 6-7: 1.3 24 a and b, 26
1.2 15, 25, 27, (43 find all the values of k and justify why these are all of them), and 49. Do not worry about getting the same answer as the back of the book (although it would be nice!) but do concentrate instead on making sure you understand the method of Gaussian Elimination.
1.1 7, 15, 19, (59 parts b and c - if it is false, provide a specific counterexample, if it is true, quote a phrase from the text), and 73.