Algebraic Geometry

Taken from Peter Stiller's What is Algebraic Geometry

Algebraic Geometry is a subject with historical roots in analytic geometry. At its most naive level it is concerned with the geometry of the solutions of a system of polynomial equations. In its early days the subject developed around the classification problem, the search for invariants of transformations, intersection problems, and the study of families of points on a curve or curves on a surface (known as linear systems). It made use of techniques from geometry (projective geometry), number theory (Diophantine equations), and analysis (elliptic and abelian integrals). Today it is a powerful synthesis of those algebraic, geometric, and analytic techniques. Results can be universally applied to a range of problems from the discrete (such as the recent proof of Fermat's Last Theorem) to the continuous (global complex analysis). It subsumes most of commutative algebra and much of algebraic number theory, and overlaps with differential geometry, modern "analytic geometry" (complex manifolds), Lie groups, representation theory, theoretical physics, and to a lesser extent the theory of partial differential equations. In addition to being one of the central disciplines of pure mathematics, algebraic geometry has developed an applied side which is linked to problems in computational complexity and the theory of algorithms, symbolic computation, robotics, control theory, computational geometry, geometric modeling, image recognition, computer vision, and scientific visualization.

Read What is Algebraic Geometry?

Adapted by Dr. Sarah from excerpts taken from Andreas Gathmann's What is algebraic geometry?

What is algebraic geometry? To start from something that you probably know, we can say that algebraic geometry is the combination of linear algebra and algebra:

In linear algebra, we study systems of linear equations in several variables.

In algebra, we study (among other things) polynomial equations in one variable.

Algebraic geometry combines these two fields of mathematics by studying systems of polynomial equations in several variables. Given such a system of polynomial equations, what sort of questions can we ask? Note that we cannot expect in general to write down explicitly all the solutions. So we are more interested in statements about the geometric structure of the set of solutions. For example, in the case of a complex polynomial equation of degree d, even if we cannot compute the solutions we know that there are exactly d of them (if we count them with the correct multiplicities). Let us now see what sort of "geometric structure" we can find in polynomial equations in several variables.

Let's look at the polynomial equation in two variables
y²=(x-1)(x-2)...(x-2n), where n is at least 1.
We can look at the set of solutions (x,y) that satisfy this equation. Recall that the complex plane is made up of numbers a + b i, where i is the square root of -1.
Question 1 Write down two real solutions that satisfy this polynomial (where x and y are both real).

Question 2 How many solutions can you find to the equation for x=0? Are these real or complex solutions? Write down these solutions.

Question 3 Let's say that n=1. Then we are looking at y²=(x-1)(x-2). How many solutions can you find to this equation for x=i? You should plug x=i into the equation and multiply out (note that i² = -1) and then solve for y. Write down these solutions.

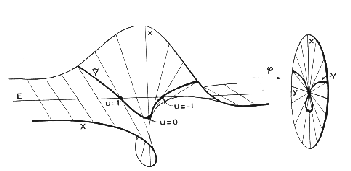
Let's go back to y²=(x-1)(x-2)...(x-2n). It is possible to write down all the solutions because the equation is (almost) solved for y already: we can pick x to be any complex numbers, and then get two values for y - unless x equals one of the roots (1, 2, 3, ... 2n) in which case we only get one value for y (namely 0).

So it seems that the set of solutions looks like two copies (a,b), (a,-b) of the complex plane with the two copies of each point 1,...,2n identified. While this is not quite true, the actual behavior is beyond the scope of this course (since the complex analysis is more difficult). So, the actual behavior is a more difficult, but we can use our naive understanding to visualize the set of solutions.

We start with two copies of the complex plane, and cut out holes to (roughly) represent the roots. We then glue the two copies of the plane together along these holes. This gives us a geometric picture of the set of solutions to this equation.

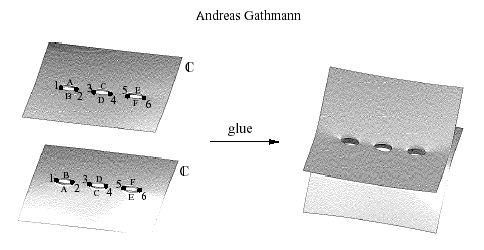
Question 4: What do we get if we instead consider y²=(x-1)(x-2)...(x-(2n-1))?
Answer questions 1 and 2 for this equation.

One of the trivial but common sources for misunderstandings is whether we count dimensions over the complex numbers (C) or the reals (R). We obtain complex curves (the dimension over C is 1) or real surfaces (the dimension over R is 2). This should help clarify the terminology from "The Proof" video that an elliptic curve (complex 1D curve that arises from a cubic, or degree 3, equation y²=x³ + ax +b ) gives a donut (real 2D surface). Skim through What is an Elliptic Curve

Let's look at a more complicated object, namely complex surfaces in 3-space (x, y, z can be complex). Look at the equation
1 + x³ + y³ + z³ - ( 1 + x + y +z)³ = 0 As the set of solutions (x,y,z) has real dimension 4, it is impossible to draw pictures of it that reflect its topological properties correctly. Usually, we overcome this problem by just drawing the real part, i.e. we look for solutions of the equation over the real numbers. This then gives a real surface in R³ that we can draw. We should just be careful about which statements we can claim to "see" from this incomplete geometric picture which shows the real part:

In contrast to our previous examples, we have now used a linear projection to map the real 3-dimensional space onto the drawing plane. We see that there are some lines contained in S. In fact, one can show that every smooth cubic surface has exactly 27 lines on it. This is another sort of question that one can ask about the solutions of polynomial equations, and that is not of topological nature: do they contain curves with special properties (in this case lines), and if so, how many? This branch of algebraic geometry is usually called enumerative geometry.

It is probably surprising that algebraic geometry, in particular enumerative geometry, is very much related to theoretical physics. In fact, many results in enumerative geometry have been found by physicists first.

What we should learn from the examples above:

Algebraic geometry can make statements about the topological structure of objects defined by polynomial equations. It is therefore related to topology and differential geometry (where similar statements are deduced using analytic methods).

The geometric objects considered in algebraic geometry need not be smooth (i.e. they need not be manifolds). Even if our primary interest is in smooth objects, degenerations to singular objects can greatly simplify a problem. This is a main point that distinguishes algebraic geometry from other "geometric" theories (e.g. differential or symplectic geometry). Of course, this comes at a price: our theory must be strong enough to include such singular objects and make statements how things vary when we degenerate from from smooth to singular objects. In this regard, algebraic geometry is related to singularity theory which studies precisely these questions.

Let's look at the example y⁵=x²-1.

Question 5: Use Maple or a graphing calculator to plot the real solutions (you can convert the equation to (x^2-1)^(1/5) if you like) with x values ranging from -100 to 100. Sketch your plot.

Question 6: Now zoom in and sketch a plot of the real solutions with x values ranging from -2 to 2. Sketch your plot.

Question 7: Now zoom in even further and sketch a plot of the real solutions with x values ranging from -1 to 1. Sketch your plot.

Question 8: In Maple, when I plot using plot((x^2-1)^(1/5),x=-1..1); there doesn't seem to be any solultions. Look back at the equation to see whether there should be. Explain.

Question 9: Take a look at these projections of the solutions. Why are they so different than your sketches?

Read What can algebraic geometry be used for?

You must complete up to this portion - if not, complete this for homework.

If time remains, then skim through The Algebraic Geometry Notebooks for Non-Experts by Aksel Sogstad . Note: If you don't have time to read this in class, then don't worry about it, as this is not homework.

Adapted by Dr. Sarah from excerpts taken from Peter Stiller's What is Algebraic Geometry, The Algebraic Geometry Notebooks for Non-Experts, Tyler J. Jarvis' Projections of Complex Algebraic Curves to Real 3-space , and Andreas Gathmann's What is Algebraic Geometry?