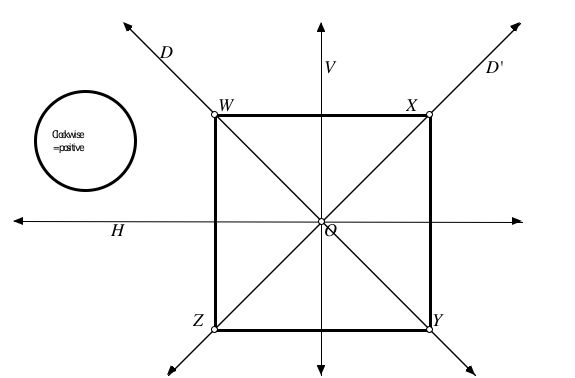
As we just saw, the 19th century work of Abel and Galois, as well as subsequent work of Cayley, Sylvester, Hamilton, Boole, etc. was the start of what is now known as ``modern'' or ``abstract'' algebra. The basic idea of modern algebra is not only to understand how to manipulate expressions, but rather to focus on the underlying algebraic structures that allow you to make those manipulations. One example of this is group theory, which (among other things) provides a way of understanding symmetry or (Euclidean) distance preserving transformations. As we learn about this algebraic structure, you will also see connections between geometry and algebra.

**The Symmetries of a Square  
The goal of this investigation is to describe all of the symmetries of a square and all of the interactions between these symmetries.  A symmetry of a square is a rigid motion of the plane which leaves the outline of the square unchanged. In other words, it is a transformation which results in a square that is superimposed onto the original square. (Note that a 90 degree rotation about the center point of a square  is a symmetry of the square, but a 45 degree rotation about the center point of a square  is not a symmetry of the square.) 

Introduction 

You will need to make a square of paper the size of the square silhouetted on this sheet of paper for your investigation.  Label the corners of the square exactly as they are labeled on the silhouette (With W, X, Y, and Z).  The back side of the square should also be labeled so that, for example, the 'Z' is directly under the 'Z' on the front side of the cut-out square. 

The HOME position of the cut-out square is a position on top of the square below, with labeled corners touching labeled corners.  When you are using the cut-out and its silhouette, it is important to describe and/or act out all rotations and reflections based on the position of the silhouette.  The descriptive points and lines on the diagram below will always be your frame of reference.   

Part 1 - DESCRIBING THE SYMMETRIES 

1.  Use words to describe  the 8 symmetries of the square.  These symmetries are written in mathematical shorthand below. 

R0

R90

R180

R270

H

V

D

D' 

2.  The rotation R90 can be thought of as a function from {W,X,Y,Z} to {W,X,Y,Z} and described by an input-output table.  The first column of the table is interpreted as follows:  Beginning with the cutout in home position, the function R90 sends vertex W of the cutout to position X of the silhouette.  Fill in the three missing outputs, and create similar input-output tables for the other seven symmetries.   

Part 2 - Describing interactions between the symmetries of the square. 

1.  We use composition of functions to define an operation on the set of the 8 symmetries of the square. 

Complete the input-output table for DR90 .     
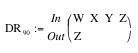Fill in the blank, DR90 =___________________   
by comparing this input-output table to the input-output tables that you created on the second page

Repeat this exercise for R90D.  
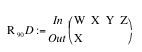            Fill in the blank: R90D = _____________   

2.  Determine the results of all of the possible compositions of the symmetries of the square.  The table that you create is called the Cayley table of a mathematical system called the group of symmetries of the square.  (The term 'group' is used here because we have a set of objects - the symmetries - and a nice binary operation  - composition of functions - on which to operate.)  What you are doing is something like creating a multiplication table. 

The Cayley Table for the Group of symmetries of a square. 

 
The symmetries of the square form a group called the dihedral group. While the development of algebraic structures and the birth of modern algebra occurred in the 19th century, the symmetries of the square were known long before that. For example, in the early 1700s, African mathematician Muhammad ibn Muhammad al-Fullani al-Kishnawi used the symmetries of the square in his work on magic squares.

Groups are algebraic structures which satisfy four properties. For example, given any two elements in a group, when we compose them, we obtain some other element of the group, such as in the Cayley table above. This property is called closure. Yet, groups do not have to be commutative. The real numbers are commutative. For the real numbers, commutativity is a property of states that when I take two numbers, a and b, then
a + b = b + a (reals are commutative under +) and
ab=ba (reals are commutative under multiplication)

3. Is the dihedral group commutative? In other words, can you find two symmetries of the square, A and B, in the Cayley table, so that AB is not BA? If so, then the group is not commutative and you should write down A, B, AB and BA.





**Adapted by Dr. Sarah from excerpts taken from Math 343: Introduction to Algebraic Structures
http://www.humboldt.edu/~dro1/new/elem/ Symmetries%20of%20SQ.doc