The Sum of the Angles of a Spherical Triangle
Let Ar be the surface area of a sphere of radius r.
A great circle divides the sphere into two congruent hemispheres.
Each of these will have area Ar / 2.
Area of a Lune
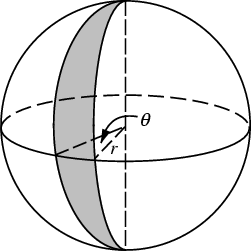
A lune is any one of the four regions determined by two
(non-coinciding) great circles. The angle of a lune is the angle
swept out by the lune as in the figure on the left.
We can measure the angle of a lune formed
between two intersecting great circles
as the angle formed by the intersection of the two defining planes
through the center of the sphere
with the plane tangent to the sphere at the point of intersection.
Imagine holding a stick straight in front of us as we walk along the first
great circle on the surface of the earth. We can measure the angle between
the tangent vectors to the curves at the given point within the tangent plane
by measuring the change of direction or angle swept out by our stick as we
turn to walk along the second great circle.
Response 1: Draw the two tangent vectors to the great circles
that sweep out the marked angle in the figure
on the right.
Use masking tape to
create two non-coinciding great circles on your beach ball as in the picture
below.
Notice that masking tape bends easily to stay on the surface
along a great circle, but it puckers if you try to turn (intrinsically)
along a curve that is not "straight".
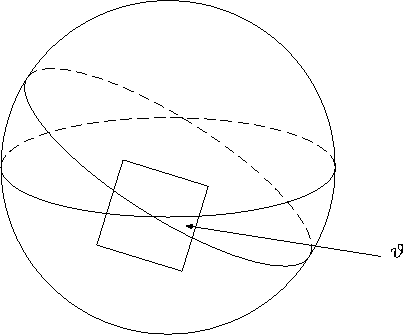
Choose a lune on your sphere as in the figure below.
Response 2: Find a formula for the area of a lune with lune angle v in
terms of v, the angle, and Ar, the surface area of the sphere.
Write down your formula here.
Hints:
What percentage angle does the lune take up out of 2 π radians?
Multiply this fraction times Ar to obtain the surface
area of the lune.
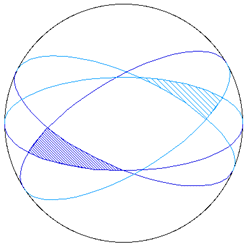
Area of a Spherical Triangle - Follow the Directions Very Carefully
Use masking tape to create a third great circle in order
to make a spherical triangle on your beach ball.
Label the vertices of your triangle A, B and C.
Label the angles of the spherical triangle as a, b and c
at the respective vertices A, B and C (ie angle a is at vertex A ...).
Fix your attention to this triangle and label its area T.
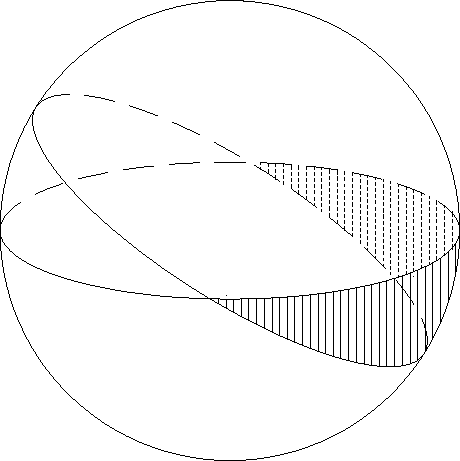
Opposite angle a is side BC. Across this side is another region on the
sphere - call its area X. Label X on your sphere.
Notice that X and T together make up a lune of angle a.
Similarly, label the area of the other region
across side AC as Y, and across side AB as Z.
Response 3:
Use your formula for the area of a lune of a given angle to write down
the areas of
T+X, T+Y, T+Z in terms of
Ar and a, Ar and b, and Ar
and c, respectively.
Response 4:
What is the sum of all of these areas,
T+X + T+Y + T+Z, in terms of Ar , a, b and c?
Show your work
here and be sure to factor out common terms.
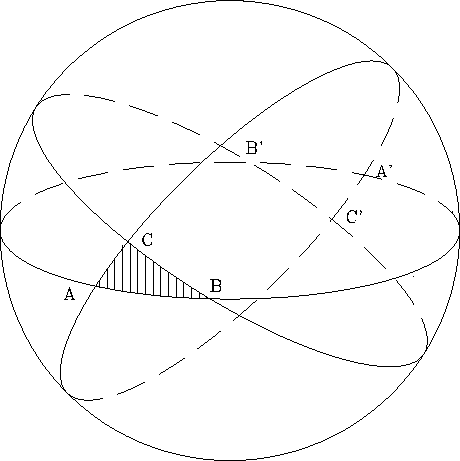
Notice that on the other side of the sphere there is another triangle
with the same area X
that is antipodal to the region you labeled as X. Label this
antipodal triangle X' on your sphere.
Response 5:
What part of the sphere does T+X'+Y+Z take up? Explain.
Response 6:
Use this to
find a formula for the area of T+X'+Y+Z in terms of just Ar.
Recall that X'=X and so this gives a formula for
T+X+Y+Z.
The formula in Response 4 gives
T+X + T+Y +T+Z = 3T + X + Y + Z in terms of a, b c and Ar.
The formula in Response 6 gives
T+X+Y+Z in terms of only Ar.
Response 7:
Subtract the formula in Response 6 from the formula in Response 4
to solve for T in terms of a, b, c and Ar.
Be sure to find a common denominator and factor out common terms.
Show work.
Sum of the Angles of a Spherical Triangle
Given any general spherical triangle T, it must have a positive area.
We can extend the sides of triangle T
to form 3 great circles. We will then obtain the situation above
and the corresponding formula for T that you just solved for.
What does the positivity of the area of the spherical triangle T
tell you about the sum of the angles? Explain and show work.






