Claim: We can construct a parallelogram that is not a square.

Tools

Arrowhead      
Point              
Compass          
Straight Edge      
Alphabet      
Script View      

Sketchpad Construction

  • Choose the Straight Edge Tool and create a segment.
  • Choose the Alphabet Tool and label the endpoints of the line A and B.
  • Choose the Compass Tool, click on A, drag the circle with your mouse and then click so that B lies on the edge of the circle centered at A.
  • Choose the Compass Tool, click on B, drag the circle with your mouse and then click so that A lies on the edge of the circle centered at B.
  • Choose the Point Tool and click down on one of the intersection points of the two circles.
  • Use the Alphabet Tool to label this intersection point as C.
  • Choose the Straight Edge Tool and create the segment AC.
  • Use the Compass Tool to create the circle that is centered at C and passes through B.
  • Use the Point Tool to create the intersection point of the circle centered at C that passes through B, and the circle that is centered at B and passes through C.
  • Use the Alphabet Tool to label this point as D.
  • Use the Straight Edge Tool to connect CD and then BD.
  • Use the Arrowhead Tool to select AB (make sure that everything else is de-selected). Under Measure, release on Length.
  • Repeat to measure the lengths of AC, CD, and BD.
  • Use the Arrowhead Tool to select C, hold down the shift key, and then select A and then B. Under Measure, release on Angle in order to measure angle CAB.
  • Repeat to measure angle ABD.
  • Move points A and B around in order to see that we still have a parallelogram that is not a square.
    Notes:
              To de-select an object, choose the Arrowhead Tool and click on the white background until the object is no longer highlighted.
              To save your work, under File, release on Save As... and save the file as anyname.gsp (for geometer's sketchpad).
              To create a script view of your work, select all of your work so that it is highlighted via Edit, Select All, and then choose the Script View Tool and release on Create New Tool. Check the Show Script View box and hit ok. To print a script view, Right-click (Windows) or Ctrl-click (Macintosh) on any object in the script, and choose Print Script View from the Context menu that appears.

    Proof of Claim - Read this along with Appendix A (p. 287-292) of Sibley

    Given segment AB, we will prove that we can construct a parallelogram that is not a square.
                                 
    Draw circle with center A and radius B. Postulate 3
    Draw circle with center B and radius A. Postulate 3
    Let C be an intersection of these circles Implicit assumption that 2 circles in the same plane intersect.
    Connect AC Postulate 1
    Connect BC. Postulate 1
    Notice that ABC is an equilateral triangle. Proposition 1 (Notice that this is exactly the same construction).
    Hence ABC has equal angles Repeated application of Proposition 5.
    Therefore angle CAB is 60 degrees Proposition 32 and Common Notions
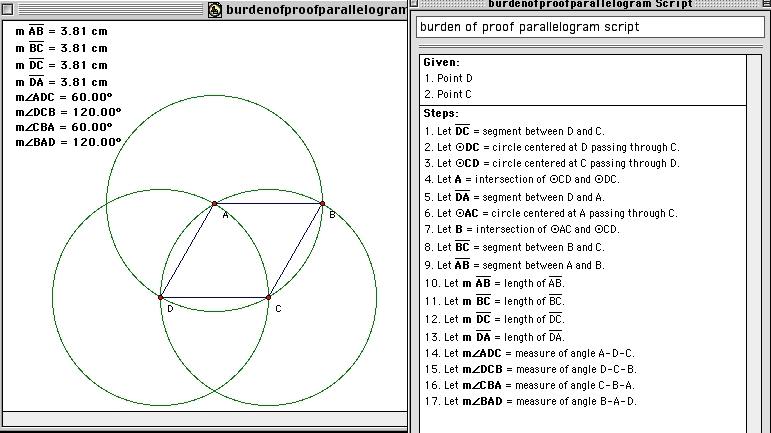
    Construct a circle with center C and radius A Postulate 3
    Let D be the intersection of this circle with the circle
    centered at B and radius C.    		 Implicit assumption that 2 circles in the same plane intersect.
    Connect CD Postulate 1
    Connect BD Postulate 1
    Notice that CD=AC Definition 15 and the fact that these are radii of the circle centered around C.
    Notice that AB=BD Definition 15 and the fact that these are radii of the circle centered around B.
    Hence CD=AC=AB=BD Common Notion 1 applied to the facts that CD=AC, AB=BD, as well as Definition 20 applied to show that AC=AB since they are sides of an equilateral triangle.
    Therefore CABD is a parallelogram that is not a square. Definition 22 and the fact that all sides are equal, but angle CAB measures 60 degrees and not 90 degrees.
    Hence, we have proven that we can construct a parallelogram that is not a square, as desired.