1. Which parametrization (patch) did you like the best?
   1. Monge patch x(u,v) = (u, v, f(u,v))
   2. geographical coordinates with 2 angles and a radius from a center like x(u,v) = (R cos u cos v, R sin u cos v, R sin v)
   3. surface of revolution x(u,v) = (g(u), h(u) cos v, h(u) sin v) from a planar curve alpha(u) = (g(u), h(u), 0)
   4. ruled surface x(u,v) = beta(u) + v delta(u), where beta and delta are curves and x(u,v) is lines emanating from the directrix beta going in the direction of delta
   5. other
   
   
   Next write down examples of surfaces for each type of parametrization.
   
   
   
   
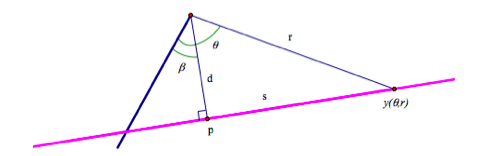
2. What is the equation of a geodesic that an arbitrary point y(theta,r) satisfies, where d and beta are defined as in the hw and following picture:
   1. theta=r
   2. r=d sec (theta-beta)
   3. r=d cos (theta-beta)
   4. d=r sec (theta-beta)
   5. arctan(s/d) = n(alpha/2)
   
   
   
   
   
   
   
3. In general on a cone of small enough cone angle, a geodesic will self-intersect...
   
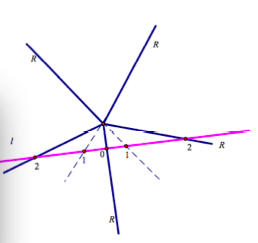
   1. they will generally not intersect
   2. at points vertically removed from each other
   3. at points horizontally removed from each other
   4. each time its lift crosses the seam of the covering
   5. infinitely many times
   
   
   

1
a: paraboloid
b: sphere
c: catenoid from catenary y=cosh(x)
e: helicoid, cone, cylinder
2. b
3. d