1. How many different geodesics are there between A and B on this 450 degree cone?
   
   1. 0
   2. 1
   3. 2
   4. 3
   5. 4
   
   
   
2. What is the equation of a geodesic that an arbitrary point y(theta,r) satisfies, where d is and beta is as in the hw sols and following picture:
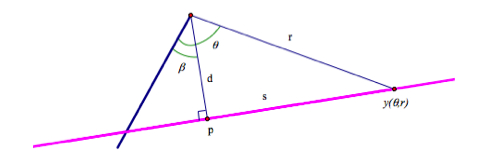
   1. theta=r
   2. r=d sec (theta-beta)
   3. r=d cos (theta-beta)
   4. d=r sec (theta-beta)
   5. arctan(s/d) = n(alpha/2)
   
   
   
3. How many times does this geodesic intersect itself?
   
   1. 0
   2. 1
   3. 2
   4. 3
   5. 4
   
   
   
4. In general on a cone of small enough cone angle, a geodesic will self-intersect...
   1. they will generally not intersect
   2. at points vertically removed from each other
   3. at points horizontally removed from each other
   4. each time its lift crosses the seam of the covering
   5. infinitely many times
   
   
   
5. On a piece of paper, in the covering plane, draw an intersecting geodesic on a flat torus.
   
   
6. On a round torus, oriented as follows, the following are geodesics:
   
   1. all vertical circles on the donut
   2. all horizonal circles on the donut
   3. both of the above
   4. none of the above
   
   
   
7. On a FLAT torus the following are geodesics:
   1. all vertical circles on the flat donut
   2. all horizonal circles on the flat donut
   3. both of the above
   4. none of the above
   
   
   
8. On a round torus, oriented as follows, a geodesic can wrap around the donut:
   
   1. just once
   2. many times
   3. both of the above
   4. none of the above
   
   
   
9. S.A. on a torus