Hypatia is the first woman mathematician about whom we have either biographical knowledge or knowledge of her mathematics. Hypatia developed commentaries on older works, probably including those by Ptolemy, Diophantus, and Apollonius, in order to make them easier to understand. Hypatia was probably the first woman to have a profound impact on the survival of early thought in mathematics.
Since Hypatia lived so long ago, it is hard to know exactly what she worked on, although we do have some specific historical evidence of her mathematics (Deakin, 1996, pp. 79-81; Fitzgerald, 1926, p. 90) and an account of her horrible death. Other fictional accounts of her life have added to the confusion about her. We do know that original scholarship was not Hypatia’s focus. Together with her father Theon, she helped preserve some of the treasures of ancient Greek mathematics and astronomy. While she cannot compare in originality with the mathematicians that she wrote commentaries on, her reputation as a teacher and scholar is secure, and as research and analysis of ancient texts continues, we may indeed learn more about her mathematical contributions.
We will examine what we do and do not know about her life, the mathematics that she might have worked on, and ways to incorporate these ideas into the mathematics classroom.
Hypatia’s Life
Hypatia’s birthdate is unknown. During the time that she lived, in the 4th century of the common era, Alexandria was the center of learning for Western civilization. According to a 6th century report by Damascius (Deakin, 1996) Hypatia was born and educated in Alexandria. She went beyond the mathematics and astronomy of her father's expertise, learning philosophy. She then taught philosophy, and presumably the prerequisite mathematics, to students who came from distant places. She was held in high esteem for her teaching, her virtue, and her civic-mindedness. There is no evidence that she traveled outside of Alexandria.
Much of what is published about Hypatia's life is fiction written in the 19th and 20th centuries. Hubbard (1908) wrote an entertaining, but fictional account of Hypatia’s educational training and life, and even invented a quote that he attributed to Hypatia. While this fictional account is highly romantic and may encourage student interest in Hypatia, there is no evidence supporting most of the tale. In her book, Osen (1974) used Hubbard as one of her primary sources on Hypatia. Unfortunately, this fictional account has been spread as truth in other publications that depend on Osen. (e.g., Johnson, 1999; Smith, 1996).
This example of mistaking fiction for fact and the spread of poor scholarship can be a great starting point for a discussion on the importance of using numerous reputable references, trying to get as close to original sources as possible, and the fact that books as well as web pages are not necessarily correct. Students will be interested in the idea that a fictional account in one book can propagate as truth, spreading to many sources.
In Hubbard’s book, he includes a fictionalized sketch of Hypatia. We have no historical basis for Hypatia’s appearance. There are no statues nor sketches of her that have survived, as far as we know. In fact, she may have resembled Egyptian women of the time instead of the woman represented as Hypatia in Figure 1. Before showing students this fictionalized sketch of Hypatia, you could ask them to imagine what Hypatia might have looked like. The fact that this fictionalized picture has been stated to be a real picture of Hypatia would also be a good beginning of a discussion of racial issues.

Figure 1. Fictionalized Sketch of Hypatia (Hubbard, 1908).
Hypatia's death in 415 is authenticated by an ancient, nearly contemporary, account of the church historian Socrates Scholasticus (Valesius, 1680; Deakin, 1996, pp. 82-84). Hypatia was an associate of Orestes, the Roman political leader of Alexandria and a rival of the Christian bishop Cyril for control of the city. Although Orestes and some of her students were Christians, Hypatia never converted to that religion. A Christian mob was incited to lynch and kill her. The mob dragged her through the streets and scraped the flesh from her bones with oyster shells before burning her body.
Smith (1996, pp. 45-46) and Lumpkin & Strong (1995, pp. 145-146) contain worksheets that engage students with questions related to Hypatia’s life and death.
Hypatia’s Mathematics
Hypatia’s reputation as the leading mathematician and philosopher of her time is authenticated in ancient writings. We have neither evidence of mathematical advances made by Hypatia, nor writings that are assuredly hers. Yet there is evidence of her commentaries on the work of others that have helped to make these older works clearer for students and to preserve them through the centuries. Let's look at the ancient evidence about Hypatia that is available, some conjectures that can be made about her mathematics, and ways to incorporate these into the classroom.
Evidence of Hypatia’s Commentaries and their Role in the Preservation of Mathematics
The one contemporaneous citation of Hypatia's mathematical work is in the introduction to Theon's commentary on Ptolemy's Book III of the Almagest. Theon describes this as "the edition having been prepared by the philosopher, my daughter Hypatia" (Rome, 1931-1943, p. 807). The other direct ancient report of Hypatia's mathematics comes from Hesychius in the 6th century: "She wrote a commentary on Diophantus, the Canon of Astronomy, and a commentary on the Conics of Apollonius" (Deakin, 1996). Since this list does not include the commentary on Ptolemy, it is obviously not exhaustive. Wilbur Knorr uses this fact and a close comparison between Hypatia's edition of the Ptolemy commentary and others by Theon to conjecture that Hypatia may well have edited and made commentaries on other ancient texts, including those of Archimedes (Knorr, 1989). Socrates Scholasticus’s report of Hypatia’s death also speaks of Hypatia's high achievements in science and philosophy, surpassing all the other philosophers of her time. We also hear of Hypatia's teaching and philosophy from one of her students, Synesius of Cyrene. His extant letters do not mention her mathematics, but he describes Hypatia as "the most holy revered philosopher" and addresses his letters to her "to the Philosopher" (Fitzgerald, 1926).
Students will be interested in the fact that detective work is needed to guess what Hypatia worked on and that historians are still debating and researching the possibilities today. They will also be interested in the role commentaries played in preserving ancient texts. These texts were written on fragile papyrus and would have disintegrated under the best of circumstances. Centuries of unrest, wars, and lack of interest in scholarship provided a poor climate for preservation. Copies of copies of copies found their way to surviving centers of culture such as Constantinople and Baghdad. Arab scholars translated ancient Greek works, wrote their own commentaries, and produced original mathematics in the Greek tradition as well. Some ancient works are known today only because of their Arabic copies, others have a Greek tradition with later commentaries as well, or in Latin translation of the Greek. Commentaries not only provided copies of ancient texts, but assistance for students who had only the text, not a teacher, from which to learn. As Western civilization fragmented and ancient schools were disbanded, those few who had access to learning were often solitary scholars. Thus Hypatia's expertise as a teacher may well have influenced untold generations.
Greek Number System
Hypatia must have used the standard Greek numbering system, which was based on the Greek alphabet, with some archaic letters included (Heath, 1921, p. 32). Each decade had a different symbol [I for tens and K for 20s, for example], but this was not a positional base-ten system. There was no use of zero, except in the base-60 fractions used in astronomy. Neither was there a subtractive principle such as the Roman's use of IV to indicate V - I. Roman influence helped solidify the standardization of the order of writing Greek numerals with the higher value on the left. In earlier times, 25 might have been written as either KE or EK.

Figure 2. Greek Number System
Hypatia’s Work on Ptolemy’s Almagest
We know that Hypatia worked on Ptolemy's Book III of the Almagest. Hence Hypatia worked in astronomy, a field that relied heavily on careful calculation and on the geometry required to describe Ptolemy's geocentric universe. The Almagest remained the leading resource for astronomical study in the West and in Arabic regions from the time of its writing in Alexandria in the second century of the common era until the time of Copernicus in the 16th century.
In Book III of the Almagest, there is a sexigesimal (base 60) computation of the orbit of the earth around the sun. Students can look at the Greek version (Knorr, 1989, pp. 802-804) and then work through a version translated into English (Knorr, 1989, pp. 780-781). It is interesting to note that in Book I, a similar computation was done very differently. Instead of the precise answer found in Book III, an approximate solution was found in Book I (see Greenwald, 2001a). In addition, stylized differences in the writing were also found. Hypatia might have worked on this section, but it also might have been Theon or someone else, and we will never know for certain.
Hypatia’s work with Diophantus
Historians have debated the extent of Hypatia's work with Diophantus. Diophantus probably lived in the third century of the common era in Alexandria. He is best known for his work Arithmetica, part of which has survived in Greek, and part only in Arabic translation. Unlike earlier mathematicians in the Greek tradition who focused on geometry and number theory, Diophantus wrote on algebra. He made innovations in introducing symbols to a field that had been one of verbal algorithms since early Babylonian times. He introduced problems with many solutions in indeterminate analysis. Hypatia's ability to teach and write commentary on these works would be an indication of her versatility as a mathematician. Although the subject matter is different from Hypatia’s known work related to astronomy and the mathematics associated with it, Diophantus was an Alexandrian mathematician, and Hypatia, as the leading mathematician of her time, must have known of his work.
There are a number of activity sheets related to Hypatia’s possible commentaries on Diophantus’ Arithmetica. Perl (1978, p. 27) engages students with the number of ways to make change for a dollar using nickels, dimes and quarters. Johnson (1999, pp. 41-42) asks students to find multiple solutions to an algebraic statement. Lumpkin & Strong (1995, pp. 144-146) discuss number patterns. Waithe (1987, pp. 176-183) contains a translation of sections from Diophantus’ Arithmetica that Hypatia might have worked on. While this is not an activity sheet, students can engage the material by translating the problems into modern algebraic notation. They can then solve them and present their work to the rest of the class.
Hypatia’s work on Apollonius’ Conics
Apollonius of Perga lived in the third century before the common era and studied in Alexandria. His work on conic sections is massive and difficult. The names of the curves parabola, ellipse, and hyperbola are his. Apollonius' work not only influenced Ptolemy in his studies of planetary orbits, but Descartes and Fermat in the 17th century in their development of analytical geometry. Any help that Hypatia gave to the elucidation and preservation of the works of Apollonius may have had far reaching consequences. The use of the Conics in astronomy and Apollonius' connection to Alexandria are arguments for Hypatia's involvement with commentaries on the Conics.
Students can investigate conic sections through a worksheet designed to engage them with both geometric and algebraic formulations of parabolas, hyperbolas and ellipses (see Perl, 1978, pp. 13-26). This worksheet encourages visualization through hands on activities such as cutting and taping sections of a cone and the exploration of each conic section as a path of points satisfying algebraic conditions. The worksheet concludes with real-life applications of conic sections.
Hypatia and Archimedes’ Dimension of the Circle
Hypatia may have written a commentary on Archimedes’ Dimension of the Circle. Archimedes, the greatest mathematician of ancient times, was killed by Roman soldiers in 212 before the common era. He lived in Syracuse, Sicily, but was in correspondence with mathematicians at Alexandria. One of his works, the Method was lost in the middle ages and only rediscovered in 1906. Another, the Dimension of the Circle is found in both Greek and Arabic copies. The Arabic manuscripts contain further clarification and careful explanation, such as might be written by a master teacher. Since Hypatia was known to be a commentator and an excellent teacher, it is certainly possible that she was one of the scholars who helped preserve this work.
Wilbur Knorr, a math historian, identified a certain style of writing that he attributes to Hypatia. He learned new languages so that he could analyze different versions of Archimedes’ Dimension of the Circle in Hebrew, Arabic, Latin and Greek. Although there is no historical evidence of the existence of commentaries developed by Hypatia on Archimedes’ work, Knorr suggests that Hypatia's influence can be found there. As research and analysis of ancient texts continues, we may learn more about Hypatia’s mathematical contributions.
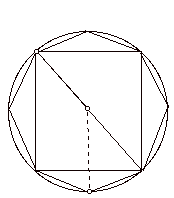
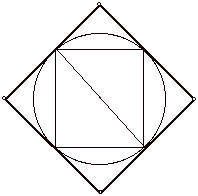
This diagram shows the inscribed polygons needed in the proof of Proposition 1: Every circle is equal to a right-angled triangle, one of whose sides containing the right angle is equal to the circumference of the circle, and the other such side equals the radius of the circle.
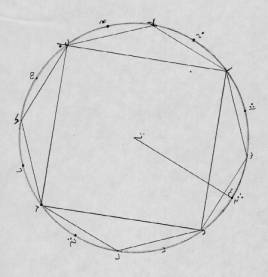
Figure 3. Arabic Diagram for Archimedes Dimension of the Circle.
The activity sheet found at the end of this column engages students with constructions related to Archimedes’ Dimension of the Circle, while a worksheet aimed at a higher level (see Greenwald, 2001b) details the proof of Proposition 1. Students can also explore these activities in a dynamic software package.