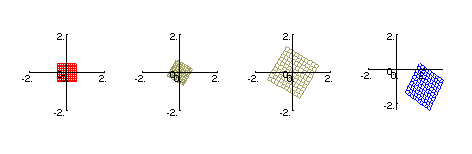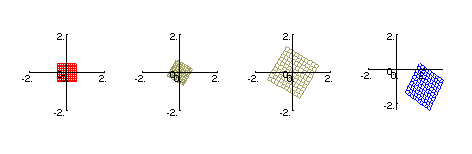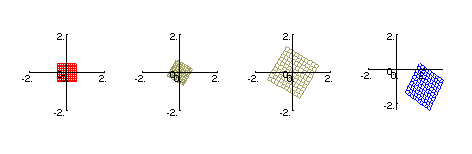Complex Linear Functions
The function is w = az+b. The blue grid is in the
z = x+iy domain, the red image is in the
w = u+iv domain.
We will consider w = (1-i) z+(2+i).
Along the real axis, think how w = az+b is
(1-i) t + (2+i) = [t+2, -t+1]
which yields the path y = -x + 3.
However, along the imaginary axis, w = az+b is
(1-i) it + (2+i) = [t+2, t+1]
which yields the path y = x - 1.
An alternative is to consider linear maps as the composition
translation(magnification(rotation)).
The linear function
w = (1+31/2i) z + (2-i)
is equal to
| z1 |
= |
eip/3 z |
(rotation) |
| z2 |
= |
2 z1 |
(magnificaton) |
| w |
= |
z2 + (2-i) |
(translation) |
This decomposition is shown acting on z = (-0.5-0.5i)..(0.5+0.5i)
in the figure below.