Convergence of Series
Wm C Bauldry
Dept of Mathematical Sciences
Appalachian State University
Series of Real Numbers
A
series
is generated by summing a sequence of terms. The
partial sums
![S[n]](Images/Series Calculator_1.gif) of the series are given by
of the series are given by ![S[n] = sum(a[i], i = n[0] .. n)](Images/Series Calculator_2.gif) . We say the series converges to a limit when the sequence of partial sums converges. Since it's very difficult to tell by inspection when a series converges, we select from a set of convergence tests that increase in power, but also increase in the effort needed for their computation. We must interpret the results of any test to determine what it tells us about the series in question.
. We say the series converges to a limit when the sequence of partial sums converges. Since it's very difficult to tell by inspection when a series converges, we select from a set of convergence tests that increase in power, but also increase in the effort needed for their computation. We must interpret the results of any test to determine what it tells us about the series in question.
The Series Test Calculator let's us enter the general term ![a[n]](Images/Series Calculator_3.gif) , the beginning index
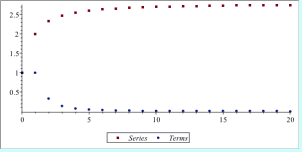
, the beginning index ![n[0]](Images/Series Calculator_4.gif) , and then have Maple perform the computations by clicking the Do the Tests button. After interpreting the results, then click the Evaluate button to see Maple's answer with a graph of the partial sums
, and then have Maple perform the computations by clicking the Do the Tests button. After interpreting the results, then click the Evaluate button to see Maple's answer with a graph of the partial sums ![S[n]](Images/Series Calculator_5.gif) and the terms
and the terms ![a[n]](Images/Series Calculator_6.gif) . Compare your results with Maple's.
. Compare your results with Maple's.
Try the Series Test Calculator with series that you know; for example, try the calculator on series with terms given by ![a[n] = `/`(1, `*`(n))](Images/Series Calculator_7.gif) and
and ![a[n] = Typesetting:-delayDotProduct(`/`(1, `*`(`^`(n, 2))), Now), factorial(explore)](Images/Series Calculator_8.gif)
The Series Test Calculator
Enter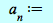  and n0 := and n0 := . Now . Now 
|
D'Alembert's Ratio Test:

|
Cauchy's Root Test:

|
Raabe's Test:

|
The Integral Test:

|
Maple's Results
|
The Series: 

|
|

|
References
- Convergence tests. From Wikipedia, the free encyclopedia.
- Convergence Tests for Infinite Series. From the "Online Mathematics Tutorials" at Harvey Mudd College.
- Choosing a Convergence Test for Infinite Series. David J. Manuel, Texas A & M University.
- List of Convergence Tests. From Wolfram MathWorld.
![S[n] = sum(a[i], i = n[0] .. n)](Images/Series Calculator_2.gif) . We say the series converges to a limit when the sequence of partial sums converges. Since it's very difficult to tell by inspection when a series converges, we select from a set of convergence tests that increase in power, but also increase in the effort needed for their computation. We must interpret the results of any test to determine what it tells us about the series in question.
. We say the series converges to a limit when the sequence of partial sums converges. Since it's very difficult to tell by inspection when a series converges, we select from a set of convergence tests that increase in power, but also increase in the effort needed for their computation. We must interpret the results of any test to determine what it tells us about the series in question.  and n0 :=
and n0 :=




