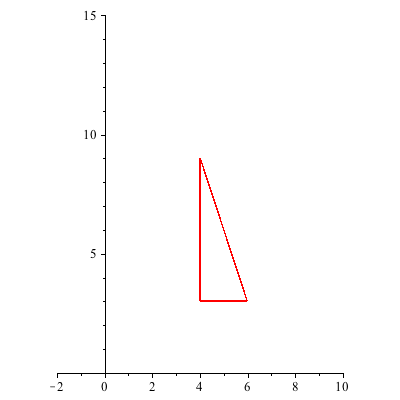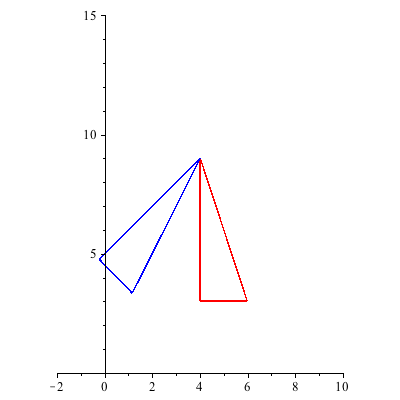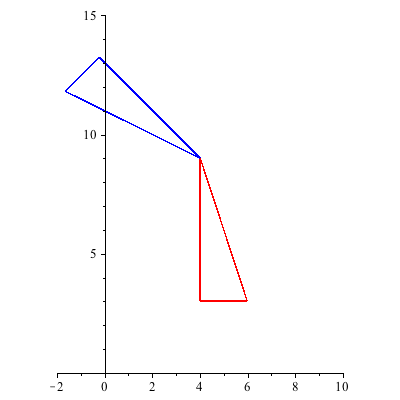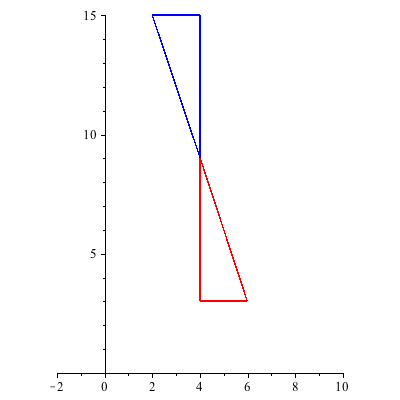
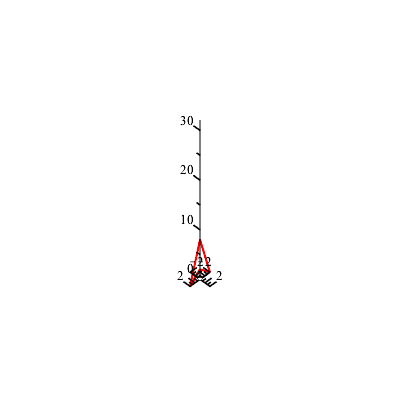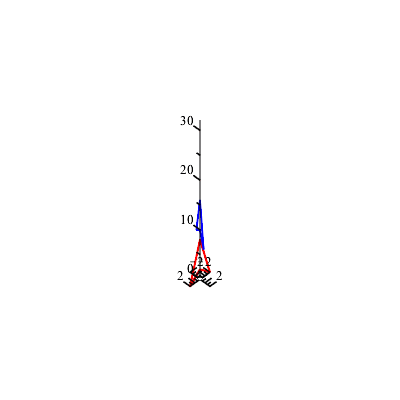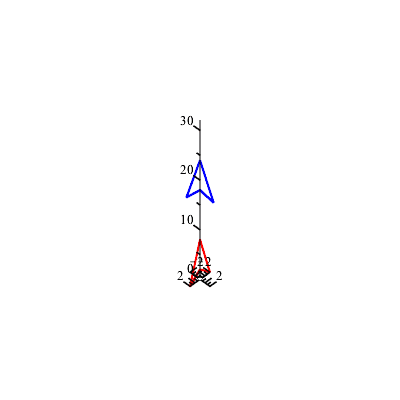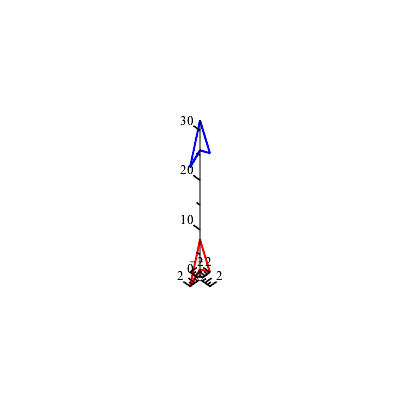
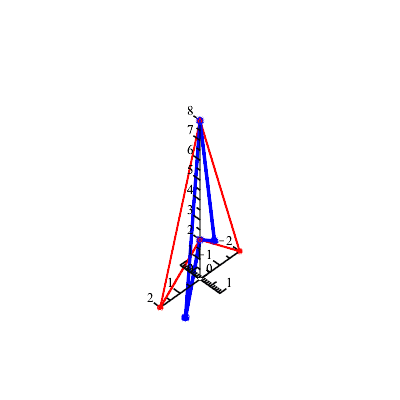
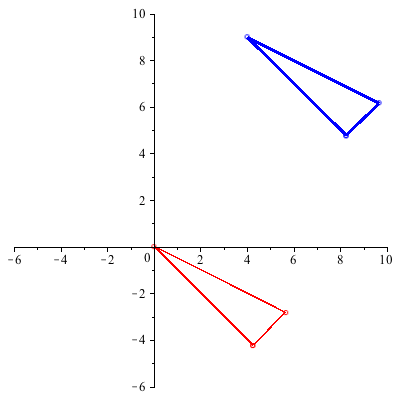
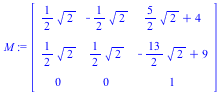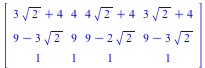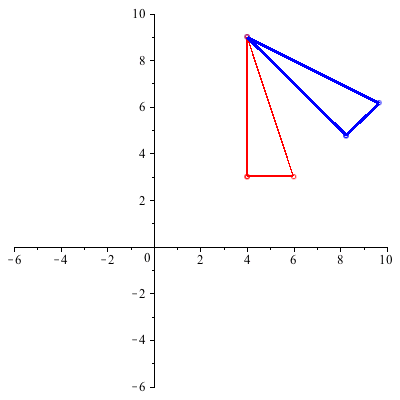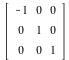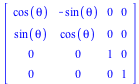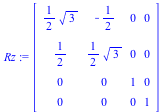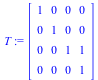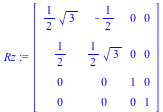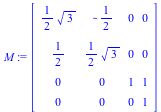Example 1: The plot below shows a red triangle with vertices (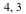 ), (
), (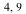 ), and (
), and (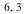 ) that has been translated up and to the right.
) that has been translated up and to the right.
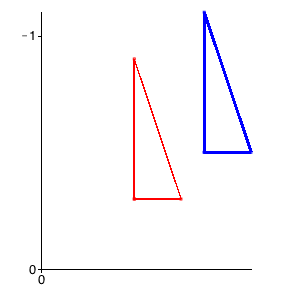
Our red triangle above can be represented using homogeneous coordinates by the matrix "triangle":
| > |
triangle := Matrix([[4,4,6,4],[3,9,3,3],[1,1,1,1]]); |
Our translation can be represented in homogenous coordinates by the translation matrix which takes each vertex ](videos/c4s5shortb_6.gif) to it's translated point (up and to the right by the vector
to it's translated point (up and to the right by the vector ](videos/c4s5shortb_7.gif) ):
):
| > |
translation:=Matrix([[1,0,3],[0,1,2],[0,0,1]]); |
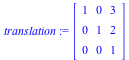 |
(1.1) |
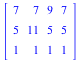 |
(1.2) |
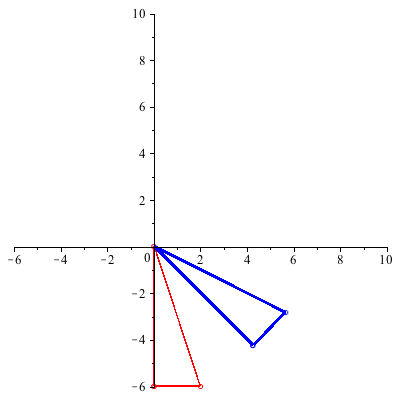
Example 2 : Rotate the triangle figure counterclockwise 45 degrees about its top vertex, (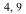 ).
).
Solution: We break the problem into the following three steps.
- Step 1. Translate the triangle so the vertex (
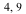 ) is at the origin.
) is at the origin.
- Step 2. Rotate the translated figure 45 degrees about the origin.
- Step 3. Translate the figure back.
Each of these steps is accomplished (see below) by applying a matrix transformation in homogeneous coordinates. The product of the three matrices gives us a single matrix that accomplishes the desired rotation in one step.
Step 1. Translate the triangle so the vertex (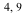 ) is moved to the origin. We therefore translate the triangle by the vector
) is moved to the origin. We therefore translate the triangle by the vector ](videos/c4s5shortb_13.gif) .
.
| > |
T := Matrix([[1, 0, -4], [0, 1, -9], [0, 0, 1]]); |
Step 2. Rotate the translated figure 45 degrees. Apply this rotation matrix R to the translated triangle, which we call "triangle1".
| > |
triangle1 := T.triangle; |
| > |
R := Matrix([[cos(Pi/4), -sin(Pi/4), 0], [sin(Pi/4), cos(Pi/4), 0], [0, 0, 1]]); |
Step 3. Translate the figure so the top vertex is moved back from (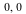 ) to (
) to (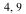 ). Apply this translation matrix U to the rotated triangle, which we call "triangle2". (Note that the translation matrices T and U are inverses of one another.)
). Apply this translation matrix U to the rotated triangle, which we call "triangle2". (Note that the translation matrices T and U are inverses of one another.)
| > |
triangle2 := R.triangle1; |
| > |
U:=Matrix([[1, 0, 4], [0, 1, 9], [0, 0, 1]]); |
Now we multiply all three matrices together (right to left, like functions) and thereby construct a single matrix that performs the rotation about the vertex (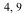 ) with a single multiplication.
) with a single multiplication.
====================
Making Movies
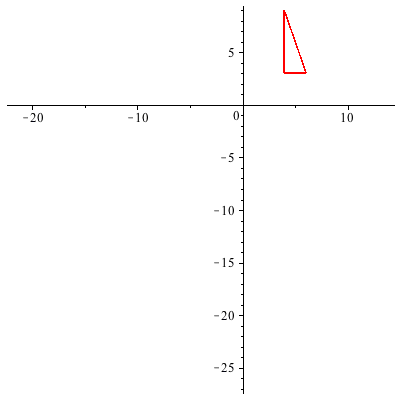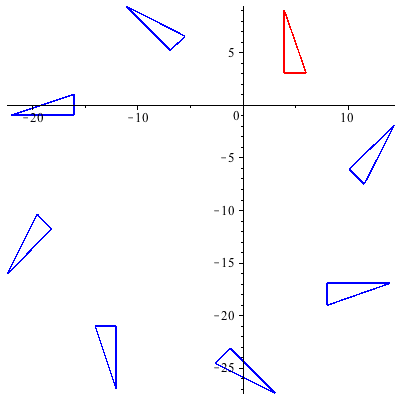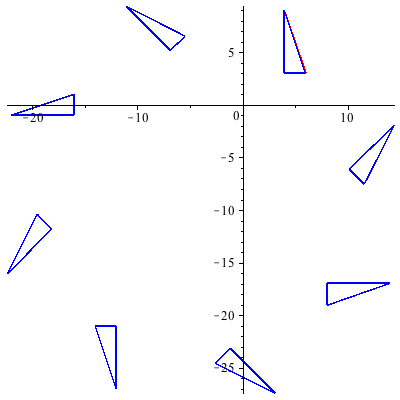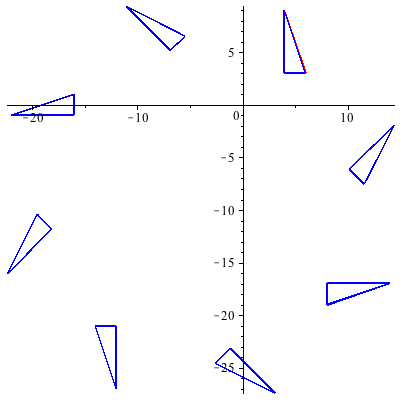
We can also apply the product matrix M repeatedly to create a simple animation: Here is a movie created by 20 frames of applying M:
Careful of the order - if I do T.R.U instead of U.R.T, we get
Example 3: Homogeneous Coordinate Transformations in 3-space
We define the homogeneous coordinates for a point ](videos/c4s5shortb_33.gif) in
in 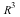 to be
to be ](videos/c4s5shortb_35.gif) . The geometric transformations of
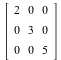
. The geometric transformations of 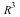 are then represented by 4 by 4 matrices. For example, here are transformations side by side with their homogeneous versions. Notice that, in each pair, the original transformation makes up the 3 by 3 block in the upper-left corner of the 4 by 4 matrix. The rest of the matrix is filled out with zeros, except for a 1 in the lower-right corner. What is the effect of each transformation in
are then represented by 4 by 4 matrices. For example, here are transformations side by side with their homogeneous versions. Notice that, in each pair, the original transformation makes up the 3 by 3 block in the upper-left corner of the 4 by 4 matrix. The rest of the matrix is filled out with zeros, except for a 1 in the lower-right corner. What is the effect of each transformation in 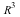 ?
?

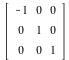

We can also create homogeneous rotation matrices for 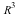 :
:
| > |
Matrix([[cos(theta), -sin(theta), 0, 0], [sin(theta), cos(theta), 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]); |
This is no longer a rotation about the origin since this is not possible in 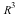 : instead we rotate about the z-axis.
: instead we rotate about the z-axis.
===================
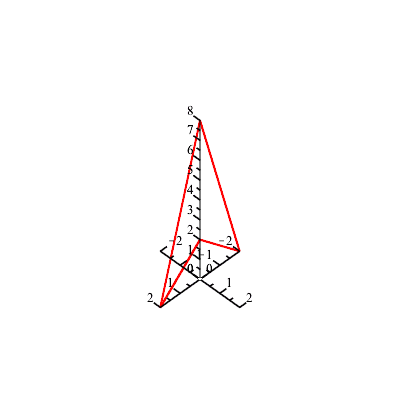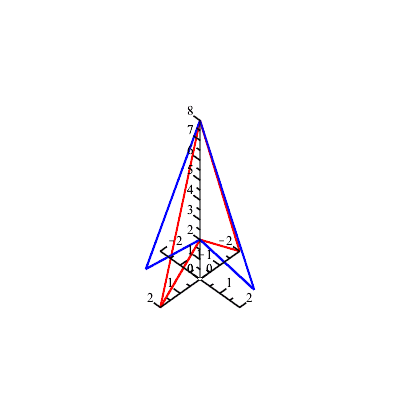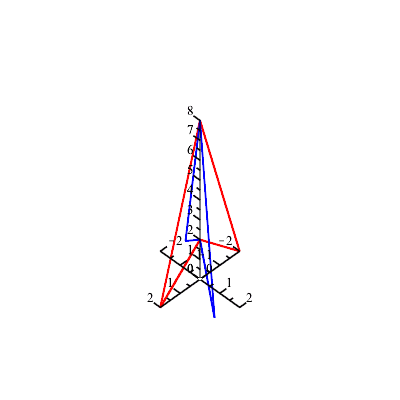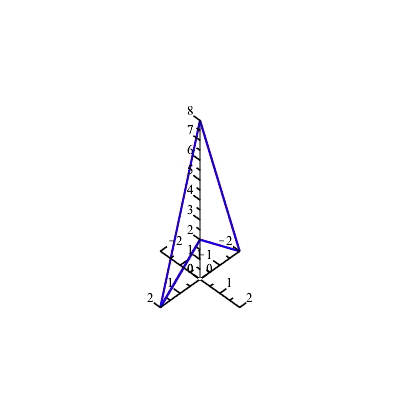
Example 4: Let's rotate a 3-D figure by 30 degrees about the z axis.
| > |
Rz := Matrix([[cos(Pi/6), -sin(Pi/6), 0, 0], [sin(Pi/6), cos(Pi/6), 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]); |
Next, let's see what happens when this rotation is applied 12 times:
==================
Example 5: Explore ~~ Here is an animation based on a composition of two matrices. Can you predict what the animation will look like before running it?
| > |
T := Matrix([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 1], [0, 0, 0, 1]]); |
| > |
Rz := Matrix([[cos(Pi/6), -sin(Pi/6), 0, 0], [sin(Pi/6), cos(Pi/6), 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]); |
24 frames:
![]() ), (
), (![]() ), and (
), and (![]() ) that has been translated up and to the right.
) that has been translated up and to the right. 
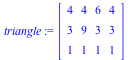
![]() to it's translated point (up and to the right by the vector
to it's translated point (up and to the right by the vector ![]() ):
): 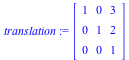
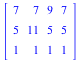
![]() ).
). 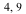 ) is at the origin.
) is at the origin. ![]() ) is moved to the origin. We therefore translate the triangle by the vector
) is moved to the origin. We therefore translate the triangle by the vector ![]() .
. 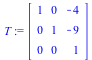
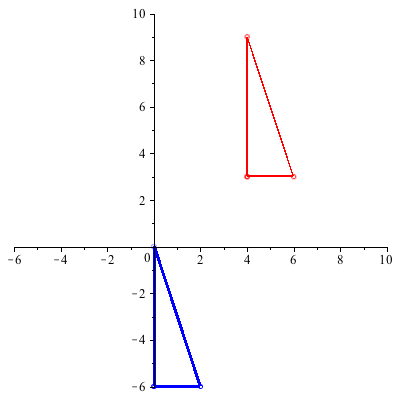
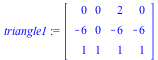
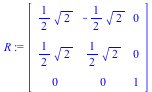
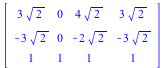
![]() ) to (
) to (![]() ). Apply this translation matrix U to the rotated triangle, which we call "triangle2". (Note that the translation matrices T and U are inverses of one another.)
). Apply this translation matrix U to the rotated triangle, which we call "triangle2". (Note that the translation matrices T and U are inverses of one another.) 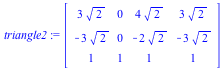
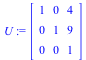
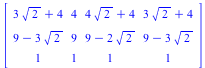
![]() ) with a single multiplication.
) with a single multiplication.