Dr. Sarah's Math 2240 Web Page - Spring 2005

  • Campus Pipeline To access WebCT (bulletin board, solutions, and grades) and to e-mail yourself attachments.
  • Direct WebCT Access if Campus Pipeline is Down
  • Syllabus and Grading Policies
  • Computer Lab Directions
  • Maple Commands and Hints for PS 1
  • Maple Commands and Hints for PS 2
  • Class highlights If you miss a class, then check here and make up the work before the next class.
    • Jump down to tomorrow's homework which is located above the red lines
    Date     WORK DUE at the beginning of class or lab unless otherwise noted! For practice problems, make sure that you can present and/or turn in your work - write out the problem and the complete solution - show work too!

    May 3 -Tues
    __________ ________________________________________________________________________
    __________

    		 ________________________________________________________________________

    Apr 28 - Thur
    • Test revisions due by 5pm

    Apr 26 - Tues
    • Final project abstract due by 11:45am as an attachment onto WebCT (text, Word, rtf, or Maple)

    Apr 21 - Thur
    Apr 18 - Mon
    • PS 6 due at 7pm - See Problem Set Guidelines and Sample Problem Set Write-Ups
      *7.1 #14 by hand and on Maple via the Eigenvectors(A); command -- also compare your answers and resolve any apparent conflicts or differences within Maple text comments.
      *Rotation matrices in R2 Recall that the general rotation matrix which rotates vectors in the counterclockwise direction by angle theta is given by
      M:=Matrix([[cos(theta),-sin(theta)],[sin(theta),cos(theta)]]);
      Part A:Use a geometric explanation to explain why most rotation matrices have no eigenvalues or eigenvectors.
      Part B: Apply the Eigenvalues(M); command. Notice that there are real eigenvalues for certain values of theta only. What are these values of theta and what eigenvalues do they produce? Find a basis for the corresponding eigenspaces. (Recall that the square root of a negative number does not exist as a real number and that cos(theta) is less than or equal to 1 always.)
      *7.2 7, 18, and 24
      *Foxes and Rabbits (Predator-prey model)
      Suppose a system of foxes and rabbits is given as: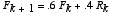


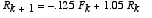
      Write out the Eigenvector decomposition of the iterate x_k, where the foxes F_k are the first component of this state vector, and the rabbits R_k the second. Use the decomposition to explain what will happen to x_k in the longterm.
      Extra Credit: Determine a value of the [2, 2] entry that leads to constant levels of the fox and rabbit populations, so that eventually neither population is changing. What is the ratio of the sizes of the populations in this case?

    Apr 14 - Thur
    • Final Project topic and annotated list of preliminary references due. Topic must be pre-approved by Dr. Sarah.

    Apr 7 - Thur
    Apr 5 - Tues
    • Review for test 2, and write down any questions you have.

    Mar 31 - Thur
    • Work on PS 6, final project, and study for the test.

    Mar 25 - Fri
    • PS 5 due at 5pm - See Problem Set Guidelines and Sample Problem Set Write-Ups
      4.3 (14 if it is a subspace then just state that it is because it is closed under addition and scalar multiplication, but if it is not, explain in detail by showing that one of these is violated, as in class. Also, as I mentioned, be sure to leave n as general - do not definite it as 2!),
      and also do 21
      VLA -- EXTRA CREDIT p. 262 #2 a, d, e, f
      4.4 12, 16, 24, 26, 53
      VLA p. 104 number 8 (**ALL IN MAPLE**) hints. This is worth more than the other problems.
      4.5 22, 24, 26, 48
      4.6 22, 24, 27, 29

    Mar 17 - Thur
    • Test 1 revisions due

    Mar 15 - Tues
    • Work on test 1 revisions and PS 5

    Mar 3 - Thur
    • Problem Set 4 Due at 5:00 pm See Problem Set Guidelines and Sample Problem Set Write-Ups
      4.1 36 and 44
      VLA p. 82#6 (*ALL IN MAPLE*) Hints for the VLA problem The VLA problem is worth more than the others.
      4.2 (19, 20, 21, 22, 31 For ALL of thse, if it is a vector space then just state that it is because it satisfies all of the vector space axioms , but if it is not, then write out the complete proof that one axiom is violated as in class)

    Mar 1 - Tues
    • Work on Problem Set 4

    Feb 24 - Thur
    • Practice Problems 4.1 numbers 7, 35, 43, 49, 52
    • Work on Problem Set 4

    Feb 22 - Tues
    • Test 1 on Chapters 1-3 Study Suggestions You can pick up your graded PS from my door after 1pm Monday.

    Feb 18 - Fri
    • Problem Set 3 See Problem Set Guidelines, Sample Problem Set Write-Ups, and the Hints for PS 3 due by 5pm
      2.510, 16, 24
      VLA 3.4 p. 158 Problem 3. Extra Credit for Problem 2.
      3.1 38, 47 a, 51
      3.2 31, 32 a and c
      3.3 (28 by-hand and on Maple), (34 -- If a unique solution to Sx=b exists, find it by using the method x=S^(-1) b.), 49, (50 a and c)

    Feb 15 - Tues
    • Read over solutions on WebCT and work on Problem Set 3.
    Feb 10 - Thur
    • Practice Problems 3.1 numbers 19, 33, 49
    • Practice Problem 3.2 number 25
    • Practice Problems 3.3 numbers 31, 35
    • Begin PS 3.

    Feb 7 - Mon
    Feb 3 - Thur
    1. Practice Problems 2.3 (5, 7, 19 by-hand)
    2. Continue Problem Set 2

    Feb 1 - Tues
    1. Practice Problems (to turn in) 2.1 numbers 7, (9 and 11 by-hand), 15, 21, 23, 25, (32 by-hand), 33, 51 and 2.2 numbers 17, 18, 35, 37
    2. Begin Problem Set 2

    Jan 27 - Thur
    1. Carefully read through Problem Set 1 Solutions on WebCT and write down any questions you have.
    2. Begin working on homework for Tues

    Jan 25 - Tues
    1. Carefully read through Select Problem Solutions for 1.1, Select Problem Solutions for 1.2, on WebCT, and Sample Problem Set Write-Ups. Write down any questions you have.
    2. Problem Set 1 Due at 5pm - See Problem Set Guidelines, Sample Problem Set Write-Ups, and Problem Set 1 Maple Commands and Hints. I also encourage you to ask me questions about anything you don't understand in office hours or on the WebCT bulletin board.
      1.1 (24 on Maple), 60, 74,
      1.2 For (30 and 32, do them by hand and also on Maple) (on Maple use no more than 3 commands to solve each problem), 44, 59, 60,
      1.3 24, 26
      c1s4.mws VLA Extra Credit VLA p. 54 #3 (Design a ski jump on Maple).

    Jan 20 - Thur
    1. Read section 1.2
    2. Practice Problems (to turn in) Larsen-Edwards 1.2 numbers 13, 15, 17, 19, 21, 25, 27, 43, 49 (do these by-hand since you need to get efficient at the by-hand method - answers to odd problems are in the back of the book - it is your job to show work).
    3. Continue working on problem set 1.

    Jan 18 - Tues
    1. Meet in 210
    2. Practice Problems (to turn in at the start of class) Larsen-Edwards 1.1 Do the following by-hand since you need practice on this (but you may use a calculator or Maple on 19 and 53) numbers 7, 15, 19, 53, 57, 59, 61, 73 (answers to odd problems are in the back of the book - it is your job to show work).
    3. Begin working on problem set 1.

    Jan 13 - Thur
    1. Read p. xv and section 1.1 in Larsen-Edwards.
    2. Begin working on practice problems in 1.1 (see Tues)