Math 2240

Dr. Sarah's Math 2240 Web Page - Summer 2005

Campus Pipeline To access WebCT (bulletin board, solutions, and grades) and to e-mail yourself attachments.

Direct WebCT Access if Campus Pipeline is Down

Syllabus and Grading Policies

Computer Lab Directions

Maple Commands and Hints for PS 1

Maple Commands and Hints for PS 2

Class highlights If you miss a class, then check here and make up the work before the next class.

Jump down to tomorrow's homework which is located above the red lines

Date	WORK DUE at the beginning of class or lab unless otherwise noted! For practice problems, make sure that you can present and/or turn in your work - write out the problem and the complete solution - show work too!
July 1 - Fri	Complete the informal course evaluation and bring it to class along with your completed poster, your final list of annotated references, and something to drink. Dr. Sarah will provide snacks, tape to attach your poster to the board/wall, etc... Final Project Poster Presentations 12:40-2:40 peer review (no need to print out the peer review form - Dr. Sarah will provide copies). poster sessions Eric Adams Olga Taussky's work with the Gersgorin Circle Theorem in calculating flutter speed of aircraft during WWII Jedidiah Bowers Neural Networks: How Learning Works Mathematically Tyler Foster Simple Image Manipulation Rachel Herron It's all about the Benjamins Christian Huffman Math Magic Brandon Johnson Computing Football Power Rankings Michael McDaniel Linear Algebra in Ancient Chinese Mathematics Cam Mullally Where muh jamz? Colemann Rusch Distributed Computing: When Maple Just Isn't Good Enough Hannah Starnes "Actions Speak Louder Than Words" Ryan Staples Fractals, Earth and Beauty Kelly Sullivan Dancing the Night Away with Matrices
__________	________________________________________________________________________
__________	________________________________________________________________________
June 30 - Thur	Final project abstract due by 12 noon as an attachment onto WebCT that I can read (text, Word, rtf, or Maple)
June 29 - Wed	Test 2 revisions due Test 3 study guide
June 28 - Tues	Final project proposal (a short description of what you plan to do) and preliminary list of references due. Your topic needs to be pre-approved as there is a limit to the number of people per topic. Study for test 3 and write down any questions you have.
June 27 - Mon	Problem Set 6 - See Problem Set Guidelines and Sample Problem Set Write-Ups *7.1 #14 by hand and on Maple via the Eigenvectors(A); command -- also compare your answers and resolve any apparent conflicts or differences within Maple text comments. *Rotation matrices in R² Recall that the general rotation matrix which rotates vectors in the counterclockwise direction by angle theta is given by M:=Matrix([[cos(theta),-sin(theta)],[sin(theta),cos(theta)]]); Part A:Use only a geometric explanation to explain why most rotation matrices have no eigenvalues or eigenvectors. Part B: Apply the Eigenvalues(M); command. Notice that there are real eigenvalues for certain values of theta only. What are these values of theta and what eigenvalues do they produce? Find a basis for the corresponding eigenspaces. 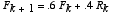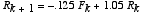(Recall that I = the square root of negative one does not exist as a real number and that cos(theta) is less than or equal to 1 always.) *7.2 7, 18, and 24 *Foxes and Rabbits (Predator-prey model) Suppose a system of foxes and rabbits is given as: Write out the Eigenvector decomposition of the iterate x_k, where the foxes F_k are the first component of this state vector, and the rabbits R_k the second. Use the decomposition to explain what will happen to x_k in the longterm. Extra Credit: Determine a value of the [2, 2] entry that leads to constant levels of the fox and rabbit populations, so that eventually neither population is changing. What is the ratio of the sizes of the populations in this case?
June 24 - Fri	Test 1 revisions due Test 2 on Chapters 1-3 and 4. Study Guide
June 23 - Thur	Review for test 2 and write down any questions you have. Read over the final project links under the July 1 due date. Begin working on Problem Set 6.
June 22 - Wed	PS 5 - See Problem Set Guidelines and Sample Problem Set Write-Ups 4.4 12, 16, 24, 26 Cement Mixing Continued (ALL IN MAPLE) hints. This is worth more than the other problems. 4.5 24, 26, 48 4.6 24, 27, 29
Jun 21 - Tues	Practice Problems (to turn in) 4.4 numbers 11, 53 4.5 number 22 4.6 numbers 22, 31 Work on Problem Set 5
June 20 - Mon	Problem Set 4 See Problem Set Guidelines and Sample Problem Set Write-Ups 4.1 36 and 44 *Cement Mixing (ALL IN MAPLE)* Hints for this problem This problem is worth more than the others. 4.2 (19 and 20 If it is a vector space then just state that it is because it satisfies all of the vector space axioms , but if it is not, then write out the complete proof that one axiom is violated as in class) Natural Numbers Prove that the natural numbers is not a subspace of R. Solutions to 2x-3y+4z=5 Prove that the subset of R³ consisting of all solutions to the equation 2x-3y+4z=5 is not a subspace of R³ 4.3 (14 parts D, E, and F if it is a subspace then just state that it is because it is closed under addition and scalar multiplication, but if it is not, explain in detail by showing that one of these is violated, as in class. Also, as I mentioned, be sure to leave n as general - do not define it as 2) Extra Credit Prove that the subset of R^5 consisting of all the solutions of the nonhomogenous equation Ax=b, where A is a given 4x5 matrix and b is a given non-zero vector in R^4 is not a subspace
Jun 17 - Fri	Test 1 on Chapters 1, 2 and 3 Study Guide
Jun 16 - Thur	Practice Problems (to turn in) 4.1 numbers 7, 35, 43, 49, 52, 4.2 numbers 21 and 22 Study for test 1 and write down any questions you have.
June 15 - Wed	Problem Set 3 See Problem Set Guidelines, Sample Problem Set Write-Ups, and the Hints for PS 3 2.5 24 Healthy/Sick Workers (on Maple) This problem is worth more than the others. 3.1* 38 and 47 a 3.2 32 a and c 3.3 (28 by-hand and on Maple), (34 -- If a unique solution to Sx=b exists, find it by using the method x=S^(-1) b.), and (50 a and c)
Jun 14 - Tues	Practice Problems (to turn in) 2.5 number 10 and 16, 3.1 number 33 (by-hand), 3.2 number 25 (by-hand), and 3.3 number 31. Work on PS 3
Jun 13 - Mon	Problem Set 2 - See Problem Set Guidelines, Sample Problem Set Write-Ups, and Maple Commands and Hints for PS 2. I also encourage you to ask me questions about anything you don't understand in office hours or on the WebCT bulletin board. 2.1 (26 by-hand and on Maple), 30 2.2 (34 parts a, b and c) To show that the following statements about matrices are false, produce counterexamples and show work: Statement a) A^2=0 implies that A = 0 Statement b) A^2=I implies that A=I or A=-I Statement c) A^2 has entries that are all greater than or equal to 0. 2.3 12, (14 by hand and on Maple), 28a, (40 parts c and d)
Jun 10 - Fri	Practice Problems (to turn in) 2.1 numbers 7, (9, 11, 15, 32 by-hand), 2.2 numbers 17, 18, 35.
Jun 9 - Thur	Problem Set 1 - See Problem Set Guidelines, Sample Problem Set Write-Ups, and Problem Set 1 Maple Commands and Hints. I also encourage you to ask me questions about anything you don't understand in office hours or on the WebCT bulletin board. 1.1 (24 on Maple), 60 b and c, 74, 1.2 (30 by hand and also on Maple), 32, 44, 59 1.3 24, 26
June 8 - Wed	Read section 1.2 Practice Problems (to turn in) Larsen-Edwards 1.2 numbers 13, 15, 17, 19, 21, 25, 27, 43, 49 (do these by-hand since you need to get efficient at the by-hand method - answers to odd problems are in the back of the book - it is your job to show work). Continue working on problem set 1.
June 7 - Tues	Read p. xv and section 1.1 Practice Problems (to turn in at the start of class) Larsen-Edwards 1.1 Do the following by-hand since you need practice on this (but you may use a calculator or Maple on 19 and 53) numbers 7, 15, 19, 53, 57, 59, 61, 73 (answers to odd problems are in the back of the book - it is your job to show work). Begin working on problem set 1.