Class Highlights
Tues May 1
Review prior to 1916 and continue with
1917 Relativity.
SpaceTime is defined by a 4D differentiable manifold, with a metric gij whose curvature tensors satisfy the Einstein field equation
for some reasonable distribution of
matter and energy.
Look at Cosmological
Considerations in the General Theory of Relativity (1917)
May 10, guidelines
Work on Exam 2 corrections, or Final Project Presentations
Thur Apr 27
Review geodesic equations, Christoffel symbols and curvatures
The Foundation of the General Theory of Relativity (1916)
Science's General Relativity: A super-quick, super-painless guide to the theory that conquered the universe.
Define the potential function and prove the Laplace equation and discuss the geometry of general relativity and Einstein's field equations from his 1916 paper.
relativity.
LIGO gravitational waves.
More evaluations.
Tues Apr 24
Review Christoffel symbols and curvatures.
Christoffel symbols and curvature tensor computations for the wormhole metric in Maple.
Research on metric forms:
-Kerr metric and Roy Kerr and Mactutor
-geodesics or curvature in Taub-NUT.
Brenton's article mentioned Exact Solutions to Einstein's Field Equations which is an e-book we can access.
Library search for it.
Other books via "Einstein field equations -- Numerical solutions" and Conformal Methods In General Relativity Index search. Web search.
Recording options [QuickTime, Camtasia...] and Homework 7
CoursEval
Work on research on Homework 7, Exam 2 corrections, or Final Project Presentations
Thur Apr 19
The Foundation of the General Theory of
Relativity (1916)
Christoffel symbols for the plane and
sphere. Definitions of curvature tensors.
Review Minkowski. Discuss null vectors in the Minkowski metric and null geodesics.
Homework 7,
CoursEval we'll take time during class on Tuesday and have some time for
research on Homework 7 or the final project
Tues Apr 17
Exam 2 corrections (turn in original test too)
Continue equations of geodesics. Introduce parallel transport--that a tangent vector stays parallel for geodesics.
Geodesics on the cone and the torus in Maple via demo from
John Oprea and modify to plotgeo(Torus,-1,1,0,2*Pi,1,2,-1,23,1.3,400,[5,24],400,100);
Relativity. Any idea of the author of the letter?
Gravity in Einstein's Universe
Tensors. Define spacetime and the Minkowski metric for special relativity. Show that free particles follow
straight line geodesics. Begin Christoffel symbols for the plane.
Thur Apr 12
Exam 2
Tues Apr 10
Gauss-Bonnet
Enneper, and
Chen-Gackstatter
first slide of geodesic equations
clicker
GC isometric constant curvature 1 surfaces by Walter Seaman
final project,
study guide
Thur Apr 5
Presentations:
- a picture of the surface
- one physically interesting feature
- one mathematician and their contributions to your surface
- one real-life application
- one MathSciNet journal article
- parametrization for your surface that can be used for the Maple worksheets
- metric form for your surface (or the start of it if it is too unwieldy) and compare
it to the flat Euclidean metric form.
- discuss Gauss curvature intuition for one interesting point on your surface
- references
Maple files of Curvatures of Surfaces Embedded in Higher Dimensions
Thur Mar 29
hyperbolic geometry, the annular model, and show that distance is exponential
Surface area of two geodesics bounded by a horocycle [r times the
length of the horocycle base].
Brioschi's K,
Gauss curvature of the annular model -1/r^2
Enneper, and
Chen-Gackstatter
Gauss Bonnet
Tues Mar 27
Computations on a cylinder, including I, II, K, and shape operator,
surface area via the metric form and the covering
surface area,
surface area on sphere, strake, and cone,
strake and I, II and K
Thur Mar 22
clickers on torus
Review fundamental forms and showhow l is derived.
Gauss and mean curvature for a torus, including 0, +, negative Gauss curvature intuition and computations.
history of Gauss and mean curvature.
Application to holding a pizza slice, minimal surfaces
area comic,
Surface area and relationship to the determinant of the metric form
Suface area on a torus.
Tues Mar 20
terminology
Applications of the first fundamental form
Local isometry: catenoid and helicoid. EFG and deformation
Examine a saddle and Enneper's surface and use E, F, G to distinguish
them even though they look the same when plotted from u=-1/2..1/2, v=-1/2..1/2.
[xu(t),xv(t)][u',v'] 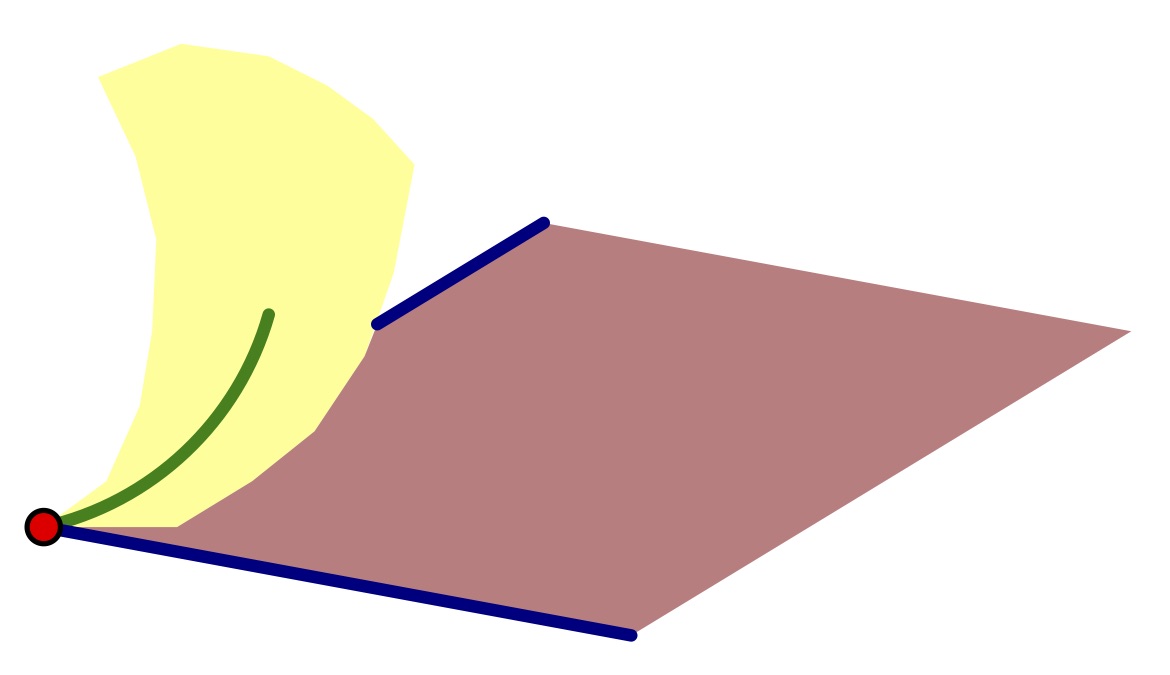
shape operator for the plane and the
sphere.
Gauss and mean curvature of a surface
Gauss' Theorem egregium: GC is intrinsic quantity.
Thur Mar 15
Show alpha' = x_u u' + x_v v' and show where E, F, and G arise and that g_ij determines dot products of tangent vectors:
First and second fundamental form slides
Clicker
Review First fundamental form in Maple and compute U and E, F, and G for geographical
coordinates on a sphere (as opposted to spherical coordinates in the Maple file)
Graphical coordinates,
spherical coordinates
Examine the Pythagorean theorem on a sphere via the metric form and then
string. Pi on a sphere.
he Maple file on geodesic and normal curvatures.
Sphere latitude:
g := (x,y) -> [cos(x)*cos(y), sin(x)*cos(y), sin(y)]:
a1:=0: a2:=Pi: b1:=0: b2:=Pi:
c1 := 1: c2 := 3:
Point := 2:
f1:= (t) -> t:
f2:= (t) -> 1:
Tues Mar 13
Vertical longitude on a cone--curvature computations and
Review Surface parametrization,
unit normal U, normal curvature and geodesic curvature
Clicker questions on cones and parametrizations
Maple file on geodesic and normal
curvatures
g := (x,y) -> [x*cos(y), x*sin(y), x]:
b2:=Pi/2:
c: 1..2, point: 1
cc:=.8497104921: dd:=-.5553603670:
f1:= (t) -> cc*sec(t/sqrt(2)+dd):
f2:= (t) -> t:
Discuss where secant comes from and where cc and dd come from
(p. 247-248) as joining the points (1,0,1) and (0,1,1).
Use the example of a plane to introduce
E, F, G and the first fundamental form/metric form
(ds/dt)2 (compare with the Pythagorean theorem).
Compare with First fundamental form in Maple
Show alpha' = x_u u' + x_v v' and work on First
and second fundamental form slides
Thur Mar 1
Cylinder computations in Maple
Clicker questions on cones #1
latitude circle - discuss why it is not a geodesic using intrinsic
arguments, including the lack of half-turn symmetry and the fact that it
unfolds to circle.
Parametrization of a cone. Explain the role of the parameters.
Review Surface parametrization,
unit normal U, normal curvature and geodesic curvature
Next examine David Henderson's Maple file:
Maple file on geodesic and normal
curvatures
g := (x,y) -> [x*cos(y), x*sin(y), x]:
a1:=0: a2:=3: b1:=0: b2:=3:
c1 := 0: c2 := 1:
Point := 1/2:
f1:= (t) -> 1/2:
f2:= (t) -> t:
latitude circle - discuss why it is not a geodesic using intrinsic arguments, including the lack of half-turn symmetry and the fact that it unfolds to
circle.
-How about verticle longitudes? Next change to:
f1:= (t) -> t:
f2:= (t) -> 1/2:
Clicker questions on cones #2-3
Geodesics on a sphere questions
Symmetry arguments on a sphere, using a toy car, lying down a ribbon
or masking tape, our feet.
Tues Feb 27
Cylindrical coordinate systems.
Equations of geos on a cylinder using trig in the covering.
Geodesic curvature and normal curvature calculations on the cylinder
speed of a geodesic and a toy car
Algebraic method of showing we have found all the geodesics on the cylinder
Discuss hw readings with a neighbor. Any questions or comments?
Maple file on geodesic and normal
curvatures adapted from David Henderson
g := (x,y) -> [cos(x), sin(x), y]:
a1:=0: a2:=2*Pi: b1:=0: b2:=Pi:
c1 := 1: c2 := 3:
Point := 2:
f1:= (t) -> t:
f2:= (t) -> sin(t):
Thur Feb 22
Review and continue geodesics on the cylinder
cone and cylinder coverings in Maple
Applications of unwrapping: surface area of a cylinder
parametrizing the cylinder via
coordinate systems:
Clicker questions on the hw readings 1-4
180 degree cone and variable cone
Tues Feb 20
isoperimetric inequality proof and applications Mention other results from the global differential geometry of curves.
Glossary on Surfaces.
Clicker question
Define manifolds,
orbifolds, surfaces, and geodesics. helix on cylinder and cone
The generalized helix on the sphere is
called loxodrome or rhumb line.
Its tangent lines have constant angle to the direction connecting the two
poles
Visual Intelligence
Continue with the cylinder. Use covering arguments to
answer questions about
the geodesics.
Thur Feb 15 Exam 1
Tues Feb 13
Clicker 1: Should the
Frenet Frame be named after
Frenet?
maple
A second argument that implies constant positive curvature in a plane is a part of a circle
to motivate the fundamental theorem of curves for the plane and R^3.
The embeddings make a difference as we'll see
when we examine curves on other kinds of surfaces. Torsion is a spacecurve construct. Replaced with other curvatures
more generally.
study guide
Given a fixed piece of string, what figure bounds the largest area? motivation, begin
isoperimetric inequality proof and applications
Thur Feb 8
Clicker #1 and #2
Constant positive curvature in a plane is a part of a circle. TNB slides.
Clicker #3 and #4
Discuss a parametrization of the strake and the annulus to motivate
surfaces.
Curvature/torsion ratio is a constant then helix.
Discuss the fundamental theorem of curves for the plane and R^3.
Tues Feb 6
Review Curve applications: Strake and more and connections to 3-D printing (once we have surfaces)
curve clicker questions
including formulas and results from last week.
TNB slides
Prove that curvature 0 iff a line. Prove that torsion 0 iff planar.
radius and curvature comic
Discuss that non-zero curvature constant for a plane curve means part of a circle.
Thur Feb 1
Clicker questions on
Rudy Rucker's How Flies Fly: Kappatau Space Curves
It is not true that a third coordinate nonzero means torsion is nonzero, via examples.
B=TxN. Since a nonplanar curve cannot be contained in a single plane,
the osculating plane changes, which means that the normal vector to the
osculating plane B changes.
Since B' is not the 0 vector and B' = -tau N, then tau can't be 0.
Desmos. +add image ballmer_peak.png. put in function on next line.
Wolfram
Demonstrations Project
Review TNB slides
T moves towards N and B moves away from N. How about N'?
Derive N' in the Frenet frame equations in two different ways.
The geometry of helices and applications. Maple commands:
with(VectorCalculus): with(plots):
helix:=<r*cos(t), r*sin(t), h*t> ;
TNBFrame(helix,t);
simplify(Curvature(helix,t));
simplify(Torsion(helix,t),trig);
spacecurve({[5*cos(t), 5*sin(t), 3*t, t = 0 .. 7]});
simplify(Curvature(helix, t)) assuming 0<h, 0<r;
simplify(Torsion(helix,t),trig) assuming 0<h, 0<r;
Twisted shirt
Curve applications: Strake and more
Torsion/curvature constant condition.
Tues Jan 30
Collect hw 2.
lolcatenary and Johann Bernoulli [1691]
Discuss a curve from #1 (or #3).
Warehouse 13's Mathematical Artifact
(32:11-33:41) and the Lemniscate of Bernoulli.
with(plots): with(VectorCalculus):
plot([(t+t^3)/(1+t^4), (t-t^3)/(1+t^4), t = -10 .. 10]);
ArcLength(<(t+t^3)/(1+t^4), (t-t^3)/(1+t^4)>, t = -10 .. 10);
simplify(Curvature(<(t+t^3)/(1+t^4), (t-t^3)/(1+t^4)>),t);
Torsion(<(t+t^3)/(1+t^4), (t-t^3)/(1+t^4),0>,t);
TNBFrame(<(t+t^3)/(1+t^4), (t-t^3)/(1+t^4),0>);
then add
assuming t::real to the TNBFrame command (look at last coordinate of B).
Examine TNBapplet.mw from -10 to -.005 and from .005 to 10.
Clicker questions on hw2
Review TNB slides
Mention that T, k and N work in higher dimensions, but the osculating
plane is not defined by a normal, nor does cross product make sense - that is
replaced by tensors and forms.
Continue deriving the Frenet equations. osculate comic
Show that B'=-tau N.
B' has no tangential component via a cross product argument, and B' has no B component via a dot
product argument.
Thur Jan 25
Clicker questions on derivatives
with respect to arc length
Calculate T and T' for a circle of arbitrary frequency.
Why the curvature vector is perpendicular to T(s) (and that the derivative of a unit vector is perpendicular to itself).
TNB slides
geom
Animated torus knot
Normal
Discuss the curvature of a circle or radius r (1/r)
and the osculating circle. B and the torsion
Clickers on curves article
MacTutor's Famous Curve Index
National Curve Bank pretzel as a curve
Wolfram's Astroid
Tues Jan 23
Note that in 1.1, v^1 versus v_1--book getting you ready for
Einstein summation notation. Lots of examples that we'll be
exploring.
Clicker question on arc
length
1.2 on arc length including proof of why regular curves can be reparamatrized
by arc length to have unit speed.
Tractrix arc length challenge by hand and using the
Maple Applet spacecurve.mw that calculates the
Velocity, Acceleration, Jerk, Speed, ArcLength, Curvature, and Torsion
Jerk and higher time derivatives.
Begin 1.3 on Frenet frames. Visualization using
Frenet Frame, and your hand,
TNB slides, T, N, curvature vector and the magnitude as a scalar.
Connect to earlier proof to explain why T(s) is a unit vector, and how chain rul comes in to computing the curvature vector from T(t)
Thur Jan 18
Hand out
glossary review: ideas from
ideas from calc 3 and linear algebra that will be helpful here.
Fill in as we go along, including within relevant hw.
Clicker questions
Talk about the hw 1 problems that the class struggles with. Solutions on ASULearn.
shortest distance comic
arc length shirt
e-book 9781614446088
Grading Policies
Tractrix. Discuss why arc length is defined as it is, and discuss local to global issues that relate.
Tues Jan 16
Course overview.
Parametrized
curves comic.
Examples of paramatrized differentiable curves in space and
Maple Applet TNBapplet.mw
Prove that alpha is a curve that is a (constant speed) straight line
iff the acceleration is 0.
Why is a line the shortest distance path between 2 points?
Our intuition might be that a curve is inefficient since it starts off
pointing away from the endpoint. However this intuition is false on a
sphere.
Prove that a line in R3 is shorter than such a curve.
